Mungkin beberapa waktu yang lalu Anda sedang mencari artikel tentang Materi Bangun Datar Gabungan di internet dan dari sekian banyak situs yang menyediakan informasi tersebut, Anda memilih untuk berkunjung ke situs ini, maka Anda sudah membuat keputusan yang tepat, karena kita memang akan mengupasnya. Baiklah langsung disimak saja yuk.
Ulasan Lengkap Materi Bangun Datar Gabungan
Untuk melengkapi artikel kami sebelumnya, kami berikan beberapa contoh soal mengenai bangun datar serta bangun datar gabungan yang sering muncul pada waktu ujian.
Simak ulasannya sampai selesai ya.
1. Rumus luas trapesium adalah…
a. ½ x alas x tinggi
b. alas x tinggi
c. ½ x (jumlah sisi sejajar) x tinggi
d. ½ x diagonal₁ x diagonal₂
Jawab:
a = luas segitiga
b = luas jajar genjang
c = luas trapesium
d = luas layang- layang atau belah ketupat
Jawaban : c
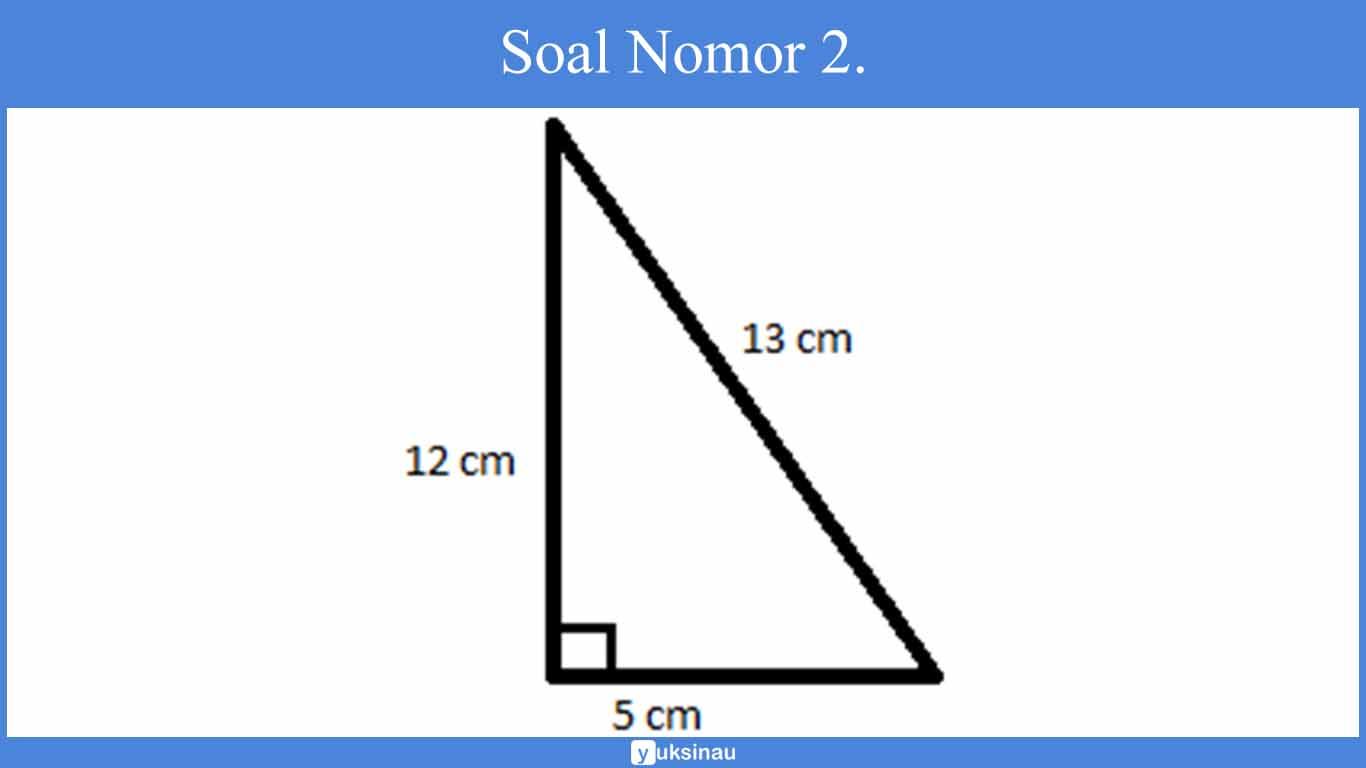
2. Keliling segitiga di bawah ini yaitu….
a. 60 cm
b. 30 cm
c. 25 cm
d. 15 cm
Jawab:
Keliling = 5 + 12 + 13
= 30 cm
Jawaban : b
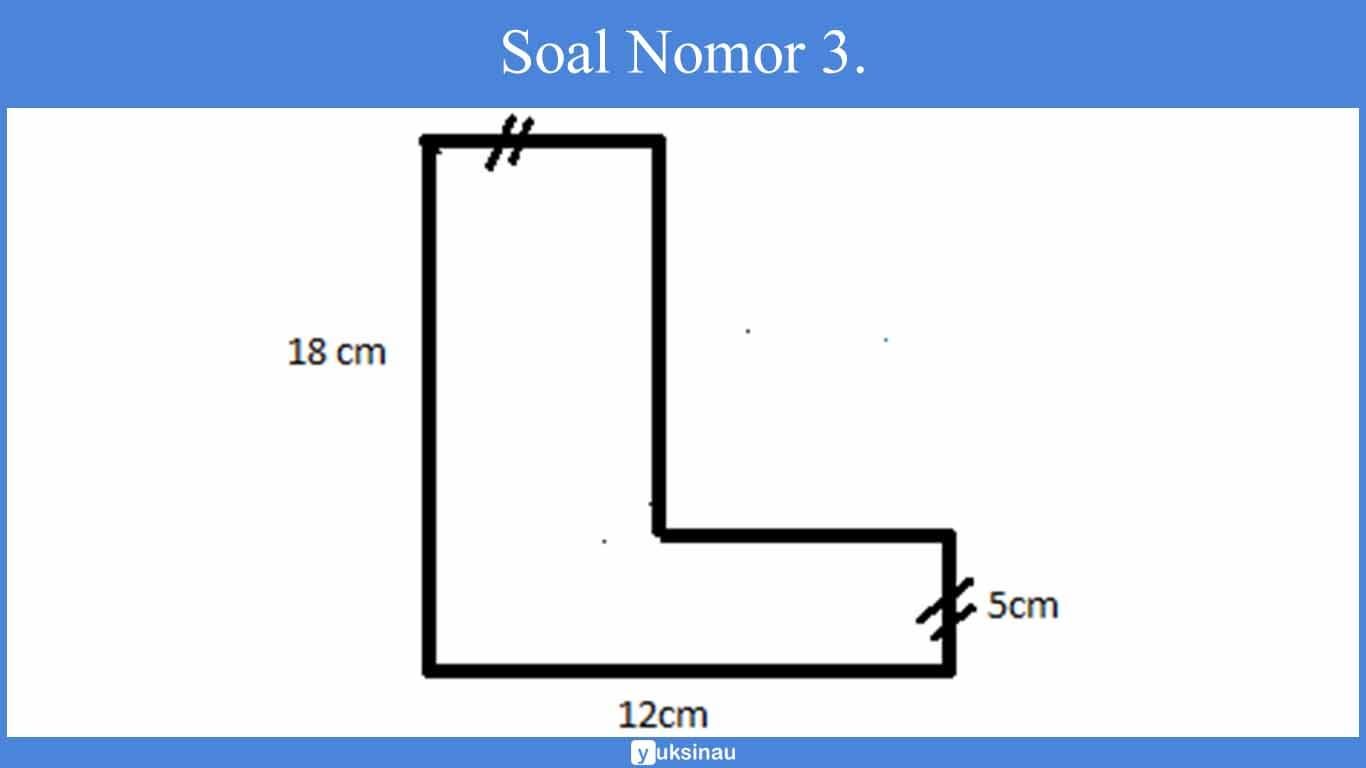
3. Keliling bangun di bawah adalah..
a. 40 cm
b. 50 cm
c. 60 cm
d. 72 cm
Jawab:
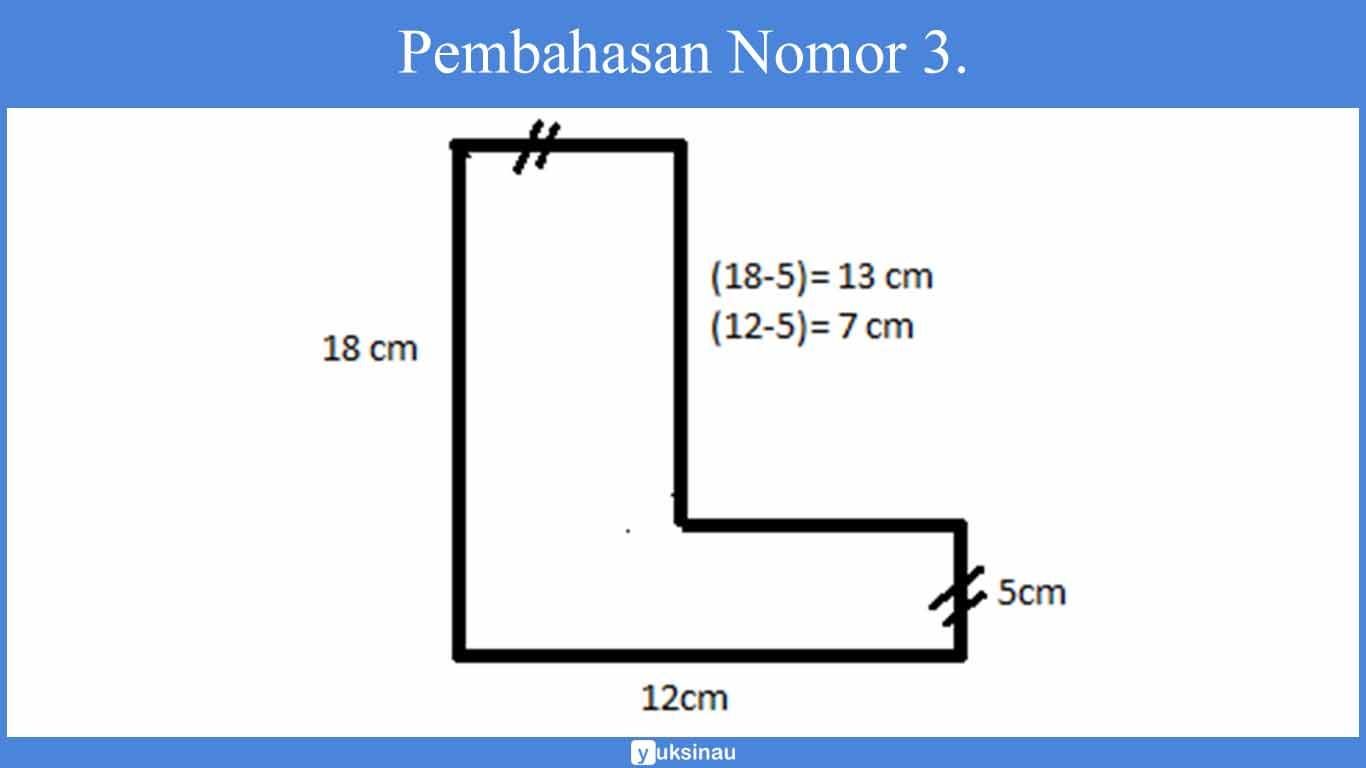
Keliling merupakan jumlah garis-garis yang membatasi suatu bangun. Keliling bangun di samping yaitu =
18 + 12 + 5 + 7 + 13 + 5 = 60 cm
Jawaban : c
4. Sebuah persegi mempunyai luas 400 cm². Berapa keliling persegi tersebut?
a. 200 cm
b. 160 cm
c. 80 cm
d. 40 cm
Jawab:
Luas persegi = s x s
maka s = √400
= 20 cm
Keliling persegi = 4 x s
= 4 x 20
= 80 cm
Jawaban: C.
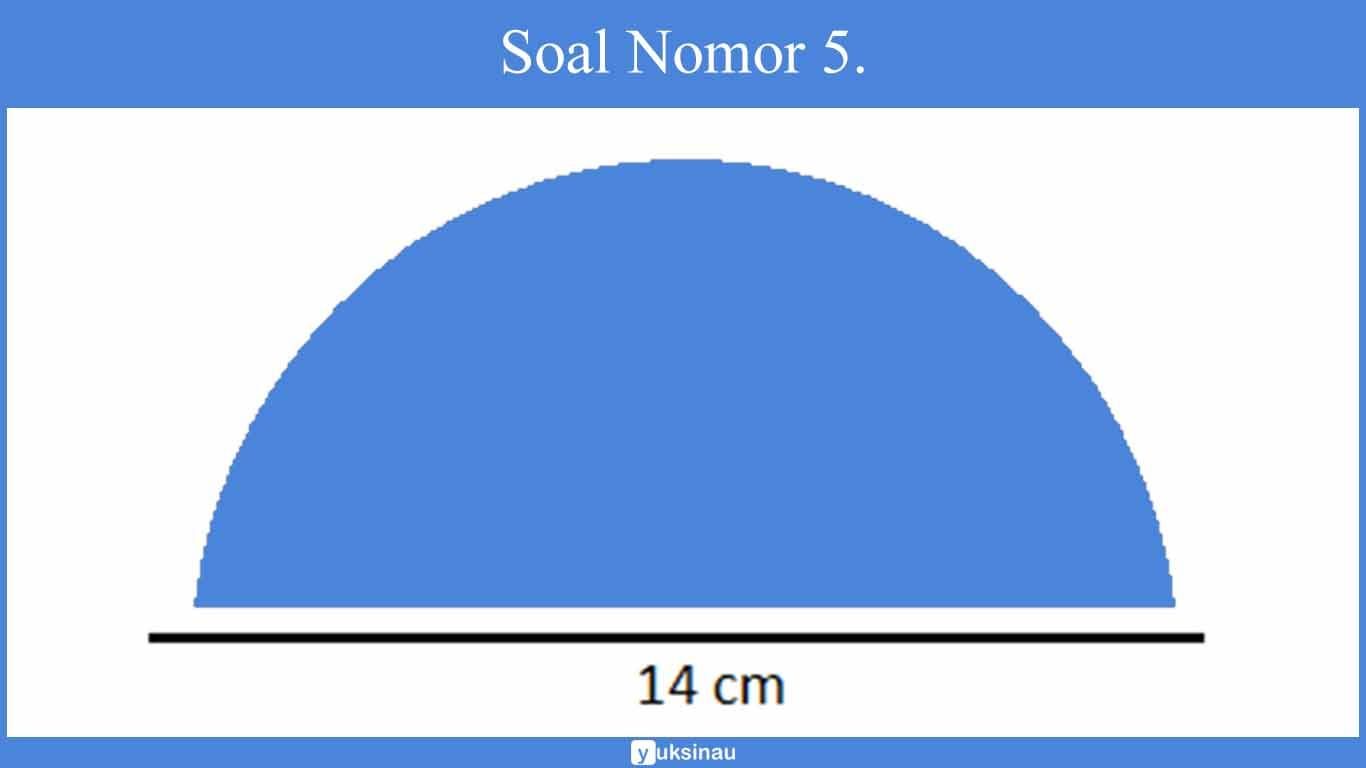
5. Keliling bangun di bawah ini adalah…
a. 11 cm
b. 22 cm
c. 33 cm
d. 36 cm
Jawab:
Garis yang membatasi ialah garis lengkung setengah keliling lingkaran serta garis datar diameter. Sehingga, keliling bangun tersebut adalah:
= (½ x л x d) + d
= (½ x ²²/₇ x 14 ) + 14
= 22 + 14 = 36 cm
Jawaban: D
6. Luas bangun di bawah yaitu …..
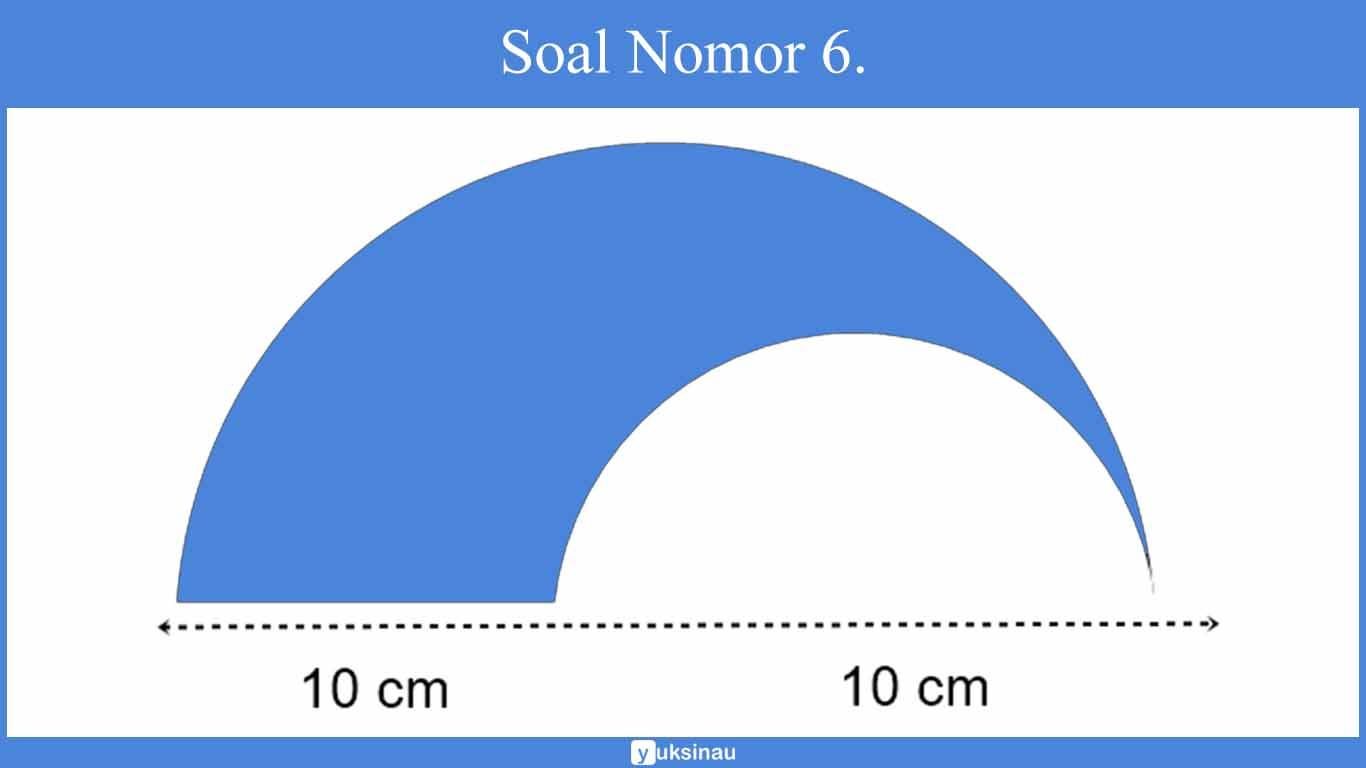
a. 39,25 cm²
b. 117,75 cm²
c. 157 cm²
d. 196,25 cm²
Jawab:
Luas I = ½ luas lingkaran besar
= ½ x л x r x r
= ½ x 3,14 x 10 x 10
= 157 cm²
Luas II = ½ luas lingkaran kecil
= ½ x 3,14 x 5 x 5
= 39,25 cm²
Luas bangun dimaksud = Luas I – Luas II
= 157 – 39,25
= 117,75 cm²
Jawaban: B.
7. Luas bangun di bawah ini adalah ….
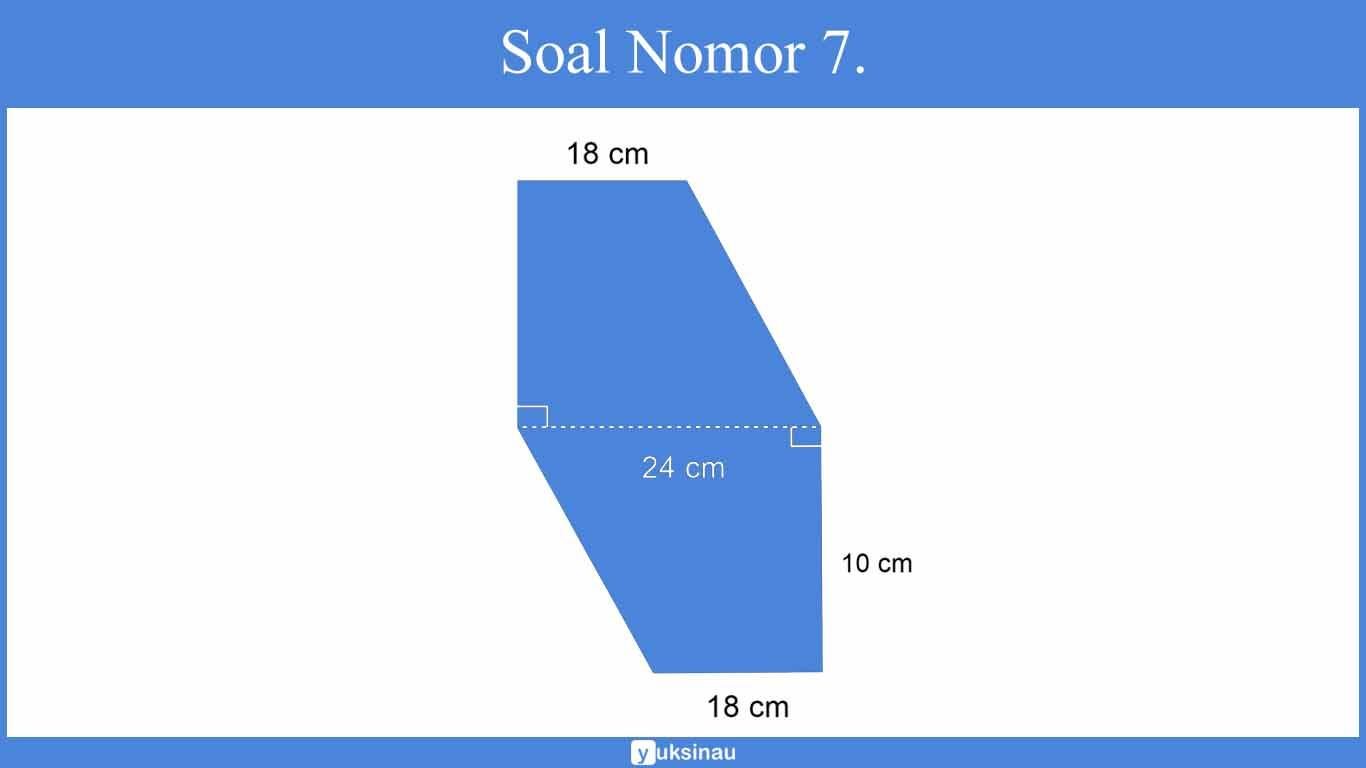
a. 210 cm²
b. 360 cm²
c. 420 cm²
d. 480 cm²
Jawab:
Bangun di atas merupakan gabungan dua trapesium siku-siku dengan ukuran:
atas (a) = 18 cm
bawah (b) = 24 cm
tinggi (t) = 10 cm
Luas I = ½ x (a+b) x t
= ½ x (18 + 24) x 10
= ½ x 42 x 10
= 210 cm²
Luas seluruhnya = 2 x 210
= 420 cm²
Jawaban: C
8. Luas bangun gabungan di bawah adalah…. cm²
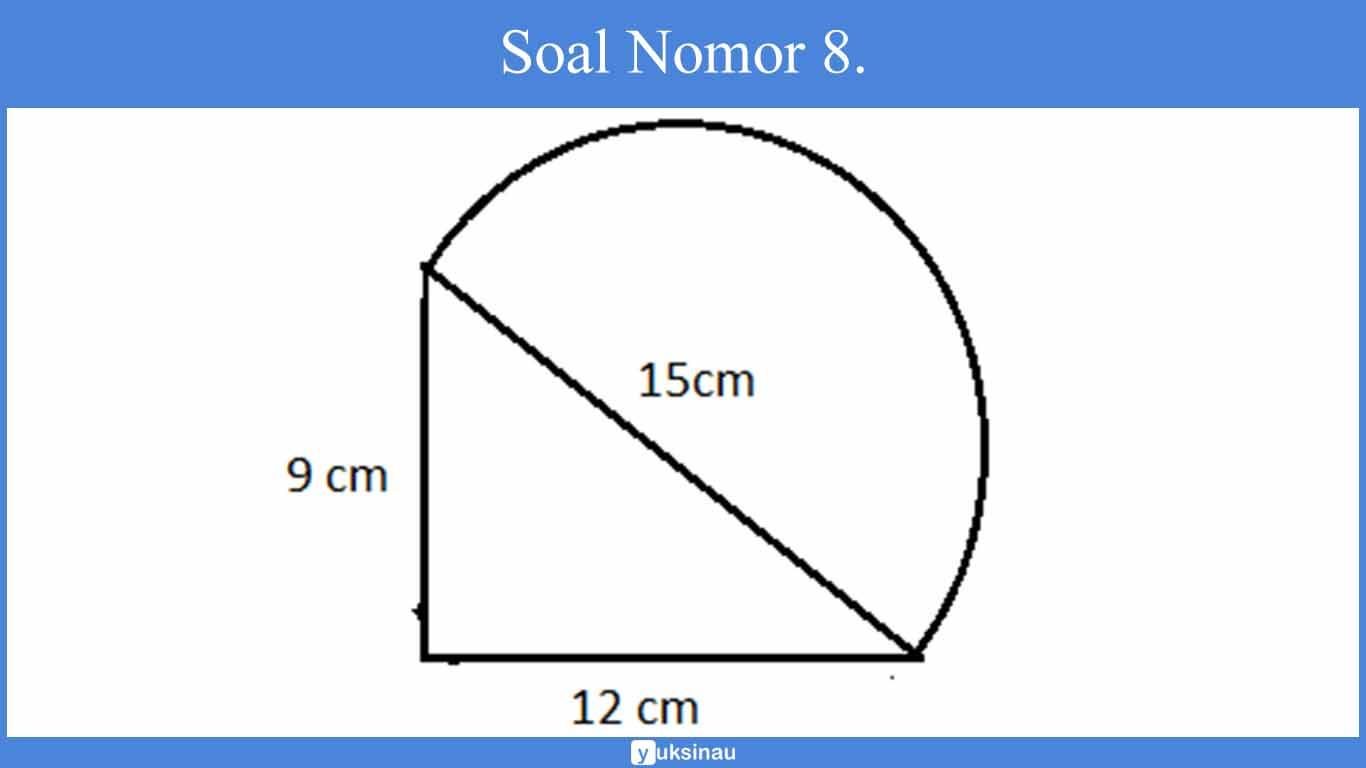
a. 54
b. 88
c. 88,31
d. 142,31
Jawab:
Bangun di atas merupakan gabungan segitiga serta setengah lingkaran
alas segitiga (a) = 12 cm
tinggi segitiga (t) = 9 cm
jari- jari lingkaran = 15 : 2 = 7,5 cm
Luas I = ½ x a x t
= ½ x 12 x 9
= 54 cm²
Luas II = ½ x л x r x r
= ½ x 3,14 x 7,5 x 7,5
= 88,31 cm²
Luas seluruhnya = Luas I + Luas II
= 54 + 88,31
= 142,31 cm²
Jawaban: D
9. Luas daerah yang diarsir pada gambar berikut adalah….
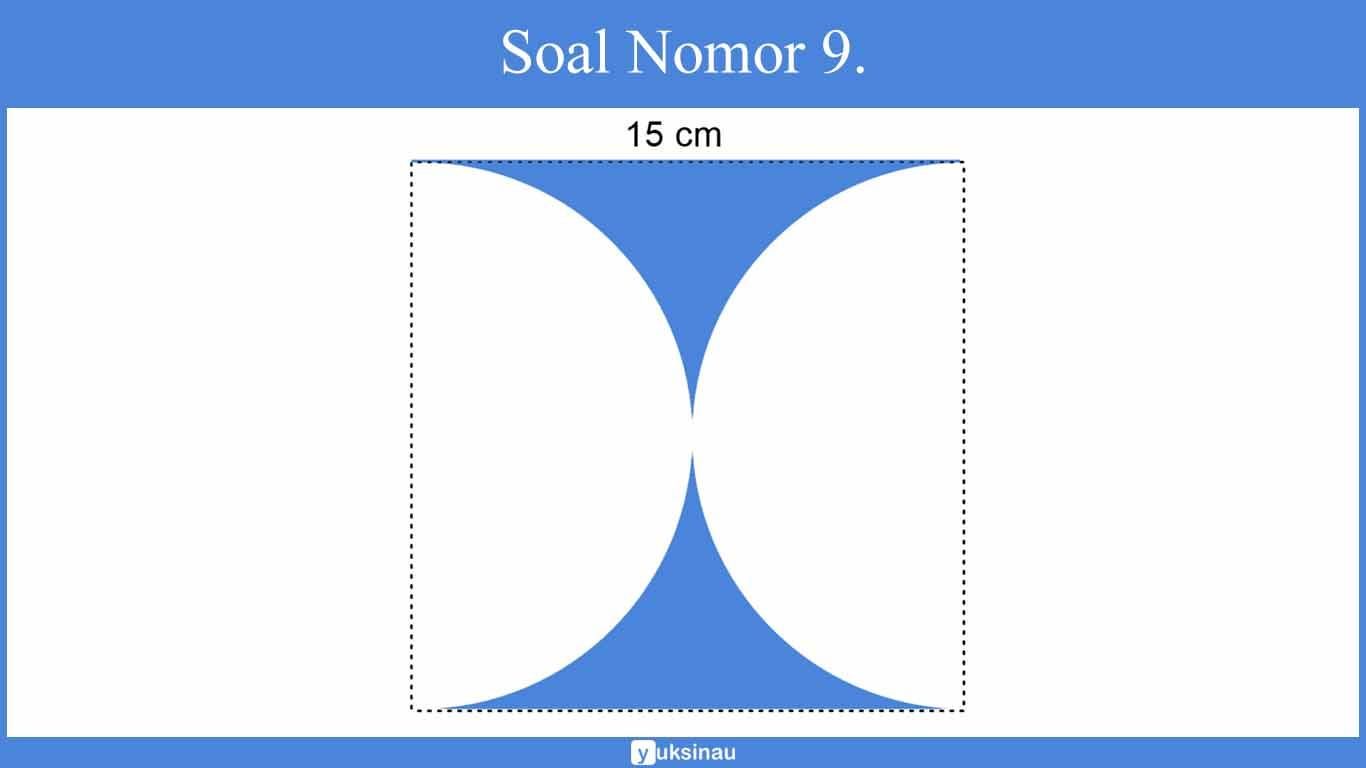
a. 48,375 cm²
b. 176,625 cm²
c. 225 cm²
d. 314 cm
Jawab:
Luas daerah yang diarsir ialah luas persegi dikurangi dengan luas sebuah lingkaran.
sisi persegi (s) = 15 cm
jari-jari lingkaran (r) = 15 : 2 = 7,5 cm
Luas I = s x s
= 15 x 15
= 225 cm²
Luas II = л x r x r
= 3,14 x 7,5 x 7,5
= 176,625 cm²
Luas daerah yang diarsir = Luas I – Luas II
= 225 – 176,625
= 48,375 cm²
Jawaban: A
10. Luas bangun ABCDEF di bawah adalah…

a. 105 cm²
b. 117 cm²
c. 124 cm²
d. 135 cm²
Jawab:
Kita bagi bangun di atas menjadi tiga bagian seperti gambar berikut
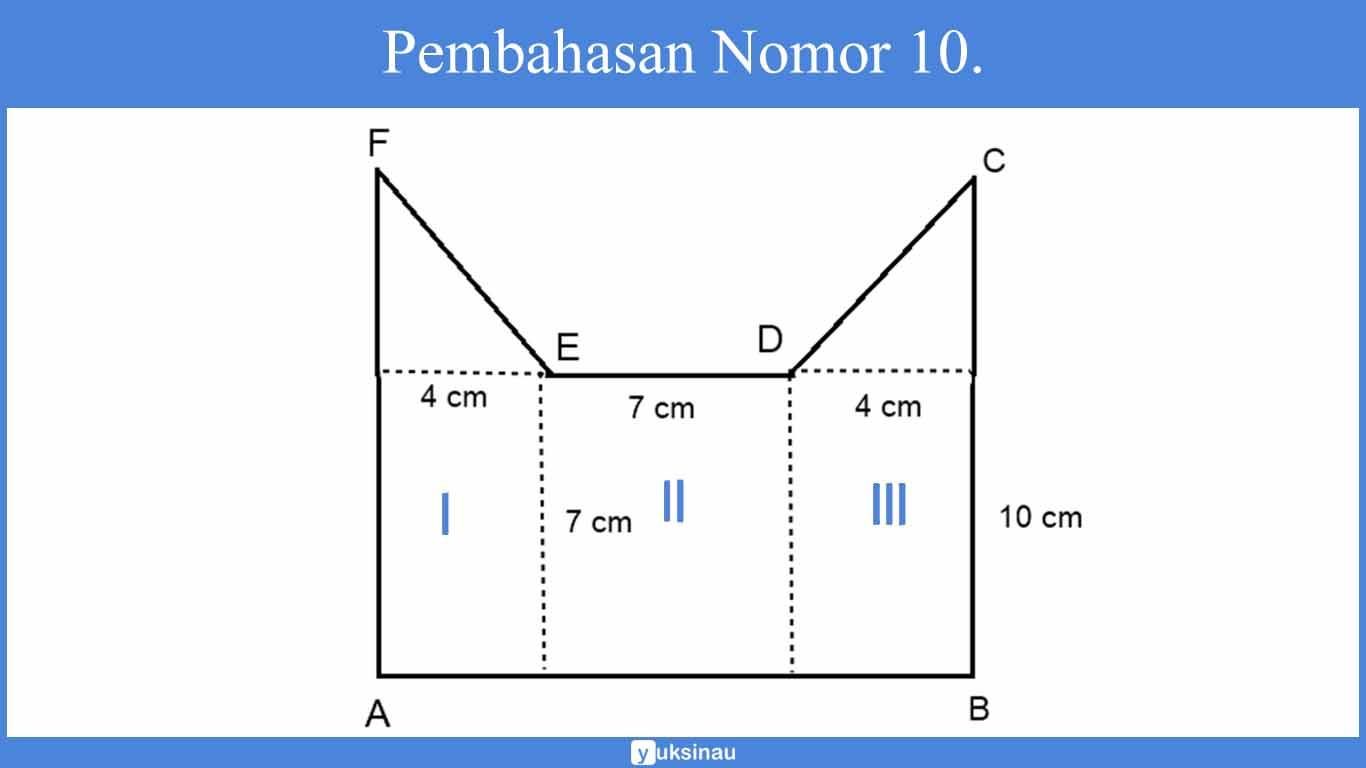
- Bangun I dan III merupakan bangun trapesium.
- Bangun II merupakan bangun persegi.
Luas I = ½ x (a+b) x t
= ½ x (7 + 10) x 4
= ½ x 17 x 4 = 34 cm²
Luas II = s x s
= 7 x 7 = 49 cm²
Luas III = ½ x (a+b) x t
= ½ x (7 + 10) x 4
= ½ x 17 x 4 = 34 cm²
Luas bangun gabungan = Luas I + Luas II + Luas III
= 34 + 49 + 34
= 117 cm²
Jawaban: B
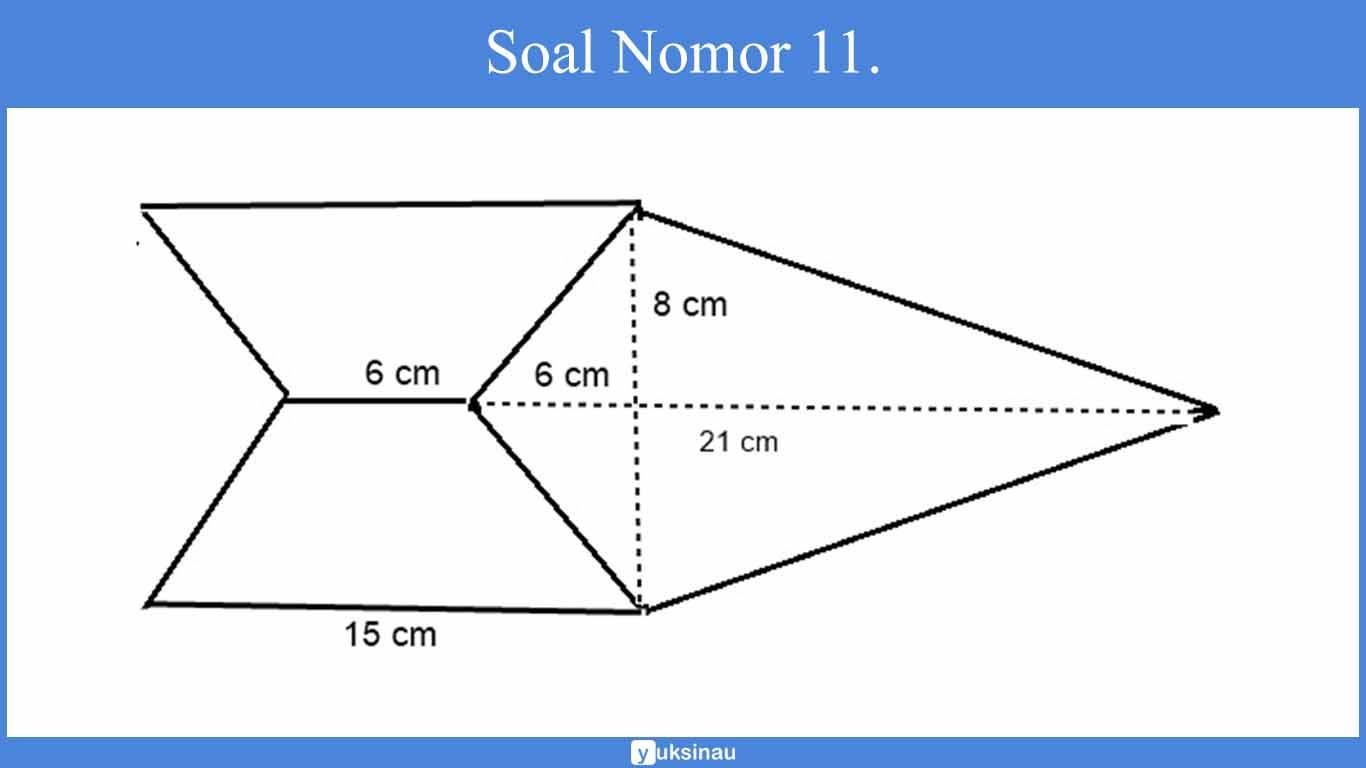
11.Luas bangun di bawah adalah…
a. 84 cm²
b. 108 cm²
c. 216 cm²
d. 384cm²
Jawab:
Langkah pertama kita bagi bangun di atas menjadi tiga bagian seperti pada gambar di bawah ini.

- Bangun I dan II merupakan trapesium dengan ukuran a = 6 cm, b = 15 cm dan t = 8 cm
- Bangun III merupakan layang-layang dengan ukuran d₁ = 8 + 8 = 16 cm dan d₂ = 6 + 21 = 27 cm
Luas I = ½ x (6+15) x 8
= ½ x 21 x 8
= 84 cm²
Luas II = ½ x (6+15) x 8
= ½ x 21 x 8
= 84 cm²
Luas III = ½ x d₁ x d₂
= ½ x 16 x 27
= 216 cm²
Luas seluruhnya = Luas I + Luas II + Luas III
= 84 + 84 + 216
= 384 cm²
Jawaban: D
12. Tentukan luas bangun berikut !

a. 48 cm²
b. 96 cm²
c. 144 cm²
d. 192 cm²
Jawab:
Bangun di atas terdiri atas dua bangun datar.
Bangun pertama merupakan jajar genjang dengan ukuran alas 12 cm serta tinggi 8 cm. Sementara, bangun kedua merupakan belah ketupat dengan ukuran d₁ = 2×8 = 16 cm dan d₂ = 2×6 = 12 cm.
Luas I = a x t
= 12 x 8
= 96 cm²
Luas II = ½ x d₁ x d₂
= ½ x 16 x 12
= 96 cm²
Luas keseluruhan = Luas I + Luas II
= 96 + 96
= 192 cm²
Jawaban: D.
13. Tentukan luas bangun berikut !

a.290,75 cm²
b.330 cm²
c.361,4 cm²
d.369,25 cm²
Jawab:
Bangun di atas merupakan suatu persegi panjang yang dipotong dengan setengah lingkaran.
Persegi panjang berukuran p = 22 cm dan lebar = 15 cm. Setengah lingkaran berukuran diameter adalah 22 – (6 +6) = 10 cm, sehingga jari-jari lingkaran = 5 cm.
Luas I = p x l
= 22 x 15
= 330 cm²
Luas II = ½ x π x r x r
= ½ x 3,14 x 5 x 5
= 39,25 cm²
Luas seluruhnya = Luas I – Luas II
= 330 – 39,25
= 290,75 cm²
Jawaban: A.
14. Keliling bangun pada nomer 13 adalah…. cm
a.48,3 cm
b.74 cm
c.79,7 cm
d.82,7 cm
Keliling = 15 + 22 + 15 + 6 + keliling ½ lingkaran + 6
= 30 + 34 + (½ x π x d)
= 64 + (½ x 3,14 x 10)
= 64 + 15,7
= 79,7 cm
15. Tentukan Luas daerah yang diarsir berikut !

a. 154 cm²
b. 224 cm²
c. 392 cm²
d. 616 cm²
Jawab:
Daerah yang diarsir merupakan bangun lingkaran yang dilubangi bangun berbentuk belah ketupat. Jari-jari lingkaran = 28 : 2 = 14 cm, sedangkan belah ketupat memiliki ukuran d₁ = d₂ = 28 cm.
Luas I = π x r x r
= ²²/₇ x 14 x 14
= 616 cm²
Luas II = ½ x d₁ x d₂
= ½ x 28 x 28
= 392 cm²
Luas daerah yang diarsir = Luas I – Luas II
= 616 – 392
= 224 cm²
Jawaban: B.
Soal Lainnya
Persegi.
Rumus Luas = sisi x sisi
= s2.
Soal 1.
Keliling suatu taman yang memiliki bentuk persegi ialah 96 m. Hitungla uas taman tersebut!
a. 575 m2.
b. 576 m2
c. 9215 m2.
d. 9216 m2.
Jawab:
Apabila keliling taman tersebut ialah 96 m maka panjang salah satu sisi dari taman tersebut yaitu 24 ( 96 : 4 = 24 ). Sehingga;
L = s x s
L = 24 x 24
L = 576 m2.
Persegi Panjang.
Rumus Luas = panjang x lebar
= p x l
Soal 1.
Gilang ingin membikin suatu bingkai foto dengan bentuk persegi panjang yang memiliki keliling 118 cm. Apabila panjang salah satu sisi bingkai foto tersebut yaitu 25 cm. Hitunglah luas dari bingkai foto tersebut!
a. 510 cm2.
b. 511 cm2.
c. 515 cm2.
d. 205 cm2.
Jawab:
Apabila keliling bingkai foto tersebut adalah 118 cm serta panjang sisi lainnya yaitu 15 cm. Maka dari itu, panjang sisi yang lain adalah 34 cm. ( 118 – 25 – 25 = 68 : 2 = 34 cm ). Sehingga;
L = p x l
L = 34 x 15
L = 510 cm2.
Segitiga.
Rumus Luas = ½ x alas x tinggi
= ½ x a x t
Soal 1.
Sebidang tanah memiliki bentuk segitiga dengan ukuran tinggi 1,8 km serta panjang sisi alas 45 m. Luas permukaan bidang tanah tersebut adalah…
a. 4000 m2.
b. 4050 m2.
c. 8000 m2.
d. 8100 m2.
Jawab:
Apabila panjang sisi alasnya 45 m serta tingginya 1,8 km. Sebab terdapat satuan m maka harus kita ubah terlebih dahulu menjadi satuan cm, sehingga akan menjadi: 1,8 km x 100 = 180 cm. Maka;
L = ½ x a x t
L = ½ x 45 x 180
L = 4050 cm2.
Jajar genjang.
Rumus Luas = alas x tinggi
= a x t
Soal 1.
Suatu taman bunga memiliki bentuk jajargenjang dengan ukuran panjang alas 93 cm serta tinggi 27 cm. Luas jajargenjang tersebut yaitu…
a. 2510 cm2.
b. 1225 cm2.
c. 2511 cm2.
d. 1226 cm2.
Jawab:
Apabila panjang alas 93 cm serta tingginya 27 cm. Maka;
L = a x t
L = 93 x 27
L = 2511 cm2.
Trapesium Soal Bangun Datar Gabungan
Rumus Luas = ½ x (atas + bawah) x tinggi
= ½ x (a + b) x t
Soal 1.
Suatu trapesium mempunyai panjang sisi atas 5 cm serta sisi bawah 10 cm. Apabila tinggi trapesium tersebut yaitu 32 cm maka luas trapesium tersebut yaitu…
a. 240 cm2.
b. 250 cm2.
c. 480 cm2.
d. 450 cm2.
Jawab:
Apabila panjang sisi atasnya adalah 5 cm, panjang sisi bawahnya adalah 10 cm, serta tingginya adalah 32 cm. Maka;
L = ½ x (a + b) x t
L = ½ x ( 5 + 10 ) x 32
L = 240 cm2.
Layang-layang Soal Bangun Datar Gabungan
Rumus Luas = ½ x diagonal1 x diagonal2
= ½ x d1 x d2
Soal 1.
Setiawan hendat membuat sebuah layang-layang yang akan diberikan untuk adiknya. Layang-layang tersebut memiliki panjang masing-masing diagonal 23 cm serta 12 cm. Luas layang-layang Gilang adalah…
a. 275 cm2.
b. 137 cm2.
c. 276 cm2.
d. 138 cm2.
Jawab:
Apabila panajang diagonal 1 nya 23 cm serta panjang diagonal 2 nya adalah 12. Mak;
L = ½ x d1 x d2
L = ½ x 23 x 12
L = 138 cm2.
Belah Ketupat Soal Bangun Datar Gabungan
Rumus Luas = ½ x diagonal1 x diagonal2
= ½ x d1 x d2
Soal 1.
Suatu perumahan terkenal yang ada di daerah Slipi berbentuk belah ketupat dengan ukuran luas 95 km. Apabila panjang salah satu diagonal perumahan tersebut ialah sepanjang 5000 m. Maka, panjang diagonal lainnya pada perumahan tersebut yaitu…
a. 35 m2.
b. 18 m2.
c. 38 m2.
d. 19 m2.
Jawab:
Apabila luas perumahan tersebut seluas 95 km serta panjang salah satu diagonalnya adalah 5000 m. Sebab terdapat satuan m, maka harus kita ubah terlebih dahulu menjadi km menjadi: 5000 : 1000 = 5 km. Maka;
L = ½ x d1 x d2
95 = 5 x X
X = 95 : 5 = 18
X = 18 cm2.
Lingkaran Soal Bangun Datar Gabungan
Rumus Luas
= π x jari x jari
= π x r2
**π = 22/7 atau 3,14
Soal 1.
Putra memiliki sebuah mobil baru yang mempunyai 4 roda. Di mana pada masing masing rodanya mempunyai jari-jari sebesar 7 cm. Luas keempat roda mobil Putra adalah…
a. 156 cm2.
b. 616 cm2.
c. 1386 cm2.
d. 2464 cm2.
Jawab:
Apabila panjang jari jari mobil Putra adalah 7 cm. Sebab yang ditanya luas dari keempat roda Putra, maka kita kalikan empat ( 7 x 4 = 28 cm ). Sehingga;
L = π x r x r
L = 22/7 x 28 x 28
L = 2464 cm2.
Baca juga: Irisan Kerucut
Demikianlah ulasan singkat terkait soal bangun datar gabungan yang dapat kami sampaikan. Semoga ulasan di atas terkait soal bangun datar gabungan dapat kalian jadikan sebagai bahan belajar kalian.
Sumber soal: https://d1ahk.blogspot.com/2018/11/soal-dan-pembahasan-bangun-datar.html
The post Materi Bangun Datar Gabungan appeared first on Yuksinau.
ARTIKEL PILIHAN PEMBACA :
Comments
Post a Comment