» Fungsi Invers - Visi Kedepan

on
Fungsi Invers - Semangat pagi! Semoga hari Anda menyenangkan dan kami ucapkan selamat datang di situs Visi Kedepan yang saat ini sedang Anda baca. Seperti yang tertulis pada judul, kali ini kita akan membahas tentang Fungsi Invers dan tentunya akan sangat menarik.

Mungkin beberapa waktu yang lalu Anda sedang mencari artikel tentang Fungsi Invers di internet dan dari sekian banyak situs yang menyediakan informasi tersebut, Anda memilih untuk berkunjung ke situs ini, maka Anda sudah membuat keputusan yang tepat, karena kita memang akan mengupasnya. Baiklah langsung disimak saja yuk.

Ulasan Lengkap Fungsi Invers

Pernahkah kamu mendengar kata kebalikan? Sebagai contoh, senang kebalikannya sedih, tinggi kebalikannya pendek dan yang lainnya.

Ternyata, dalam matematika juga dikenal istilah kebalikan lho. Kebalikan pada matematika ini terdapat pada fungsi, khusunya pada fungsi invers.

Lantas, apakah yang disebut sebagai fungsi invers? Simak pembahasannya berikut ini.

Fungsi Invers

Fungsi invers atau yang juga dikenal sebagai fungsi kebalikan adalah sebuah fungsi yang berkebalikan dari fungsi asalnya.

Sebuah fungsi f mempunyai fungsi invers (kebalikan) f-1 jika f adalah fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut bisa dinyatakan seperti berikut:

(f-1)-1 = f

Simplenya, fungsi bijektif berlangsung pada saat jumlah anggota domain sama dengan jumlah anggota kodomain.

Tidak terdapat dua atau lebih domain berbeda dipetakan ke kodomain yang sama. Serta pada setiap kodomain mempunyai pasangan di domain. Perhatikan gambar yang ada di bawah ini:

invers komposisi

Berdasarkan gambar dari pemetaan di atas, pemetaan pertama menunjukan fungsi bijektif.

Pemetaan kedua bukan merupakan fungsi bijektif sebab pemetaan tersebut hanya berlangsung fungsi pada.

Domain d dan e dipetakan ke anggota kodomain yang sama. Pemetaan ketiga bukan fungsi bijektif sebab pemetaan tersebut hanya berlangsung pada fungsi satu-satu. Kodomain 9 tidak mempunyai pasangan pada anggota domain.

Sebagai contoh, f fungsi yang memetakan x ke y, sehingga bisa kita tulisakan menjadi y = f(x), maka f-1 merupakan fungsi yang memetakan y ke x, ditulis x = f-1(y).

Misalnya f : A →B fungsi bijektif. Invers fungsi f merupakan fungsi yang mengawankan pada masing-masing elemen B dengan tepat satu elemen pada A.

Invers fungsi f juga dinyatakan dengan f-1 seperti di bawah ini:

materi invers

Terdapat 3 tahapan untuk menentukan fungsi invers, antara lain:

  1. Ubahlah bentuk y = f(x) menjadi bentuk x = f(y).
  2. Tuliskan x sebagai f-1(y) sehingga f-1(y) = f(y).
  3. Ubahlah variabel y dengan x sehingga akan didapatkan rumus fungsi invers f-1(x).

Dalam fungsi invers ada rumus khusus seperti berikut ini:

invers pecahan

Fungsi & Komposisi

Aljabar Fungsi

1. Penjumlahan f dan g

(f + g) (x) = f(x) + g(x).

Contoh Soal:

Diketahui f(x) = x + 2 dan g(x) = x2 – 4. Tentukan (f + g)(x).

Jawab:

(f + g)(x) = f(x) + gx)
(f + g)(x)= x + 2 + x2 – 4
(f + g)(x)= x2 + x – 2

2. Pengurangan f dan g

(f – g)(x) = f(x) – g(x).

Contoh soal

Diketahui f(x) = x2 – 3x dan g(x) = 2x + 1. Tentukan (f – g)(x).

Jawab:

(f – g)(x) = f(x) – g(x)
(f – g)(x)= x2 – 3x – (2x + 1)
(f – g)(x)= x2 – 3x – 2x – 1
(f – g)(x)= x2 – 5x – 1

3. Perkalian f dan g

(f . g)(x) = f(x) . g(x).

Contoh soal

Diketahui f(x) = x – 5 dan g(x) = x2 + x. Tentukan (f × g)(x).

Jawab:

(f × g)(x) = f(x) . g(x)
(f × g)(x)= (x – 5)(x2 + x)
(f × g)(x)= x3 + x2 – 5x2 – 5x
(f × g)(x)= x3 – 4x2 – 5x

4. Pembagian f dan g
Pembagian f dan g

Contoh soal

Diketahui f(x) = x2 – 4 dan g(x) = x + 2. Tentukan

pembagian fungsi invers

Jawab:

jawaban Pembagian f dan g

Fungsi Komposisi

Fungsi komposisi bisa kita tuliskan seperti berikut ini:

(f ◦ g)(x) = f (g (x))→ komposisi g (fungsi f bundaran g atau fungsi komposisi dengan g dikerjakan terlebih dahulu daripada f)

gambar 7

(g ◦ f)(x)= g (f (x))→ komposisi f (fungsi g bundaran f atau fungsi komposisi dengan f dikerjakan terlebih dahulu daripada g)

sifat invers

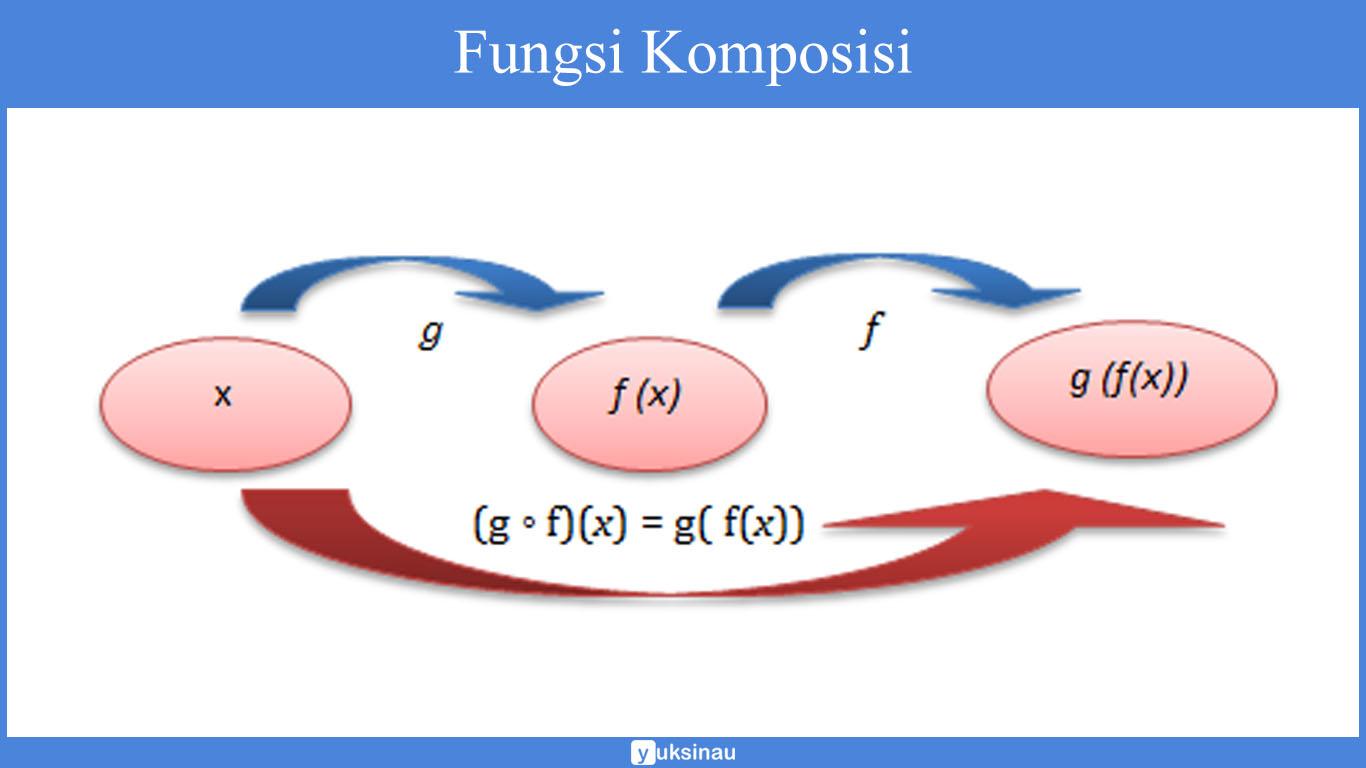
Sifat Fungsi Komposisi

  1. Tidak berlaku sifat komutatif, (f ◦ g)(x) ≠ (g ◦ f)(x).
  2. Berlaku sifat asosiatif, (f ◦(g ◦ h))(x) = ((f ◦ g)◦ h)(x).
  3. Adanya unsur identitas (l)(x), (f ◦ l)(x) = (l ◦ f)(x) = f(x).

Contoh soal:

Diketahui f(x) = 2x – 1, g(x) = x2 + 2. Maka tentukan:

  1. (g ◦ f)(x).
  2. (f ◦ g)(x).
  3. Apakah berlaku sifat komutatif: g ◦ f = f ◦ g?

Jawab:

  1. (g ◦ f)(x) = g(f(x)) = g(2x – 1) = (2x – 1)2 + 2 = 4x2 – 4x + 1 + 2 = 4x2 – 4x + 3
  2. (f ◦ g)(x) = f(g(x)) = f(x2 + 2) = 2(x2 + 2) – 1 = 4x2 + 4 – 1 = 4x2 + 3
  3. Tidak berlaku sifat komutatif sebab g ◦ f ¹ f ◦ g.

Fungsi Invers

1. f-1 (x) adalah invers dari fungsi f(x)

invers kuadrat

2. Menentukan fungsi invers : mengganti f (x)= y = …” menjadi “ f -1 (y)= x = …”

3. hubungan sifat fungsi invers dengan fungsi komposisi:

  1. (f ◦ f-1)(x)= (f -1 ◦ f)(x)= l (x)
  2. (f ◦ g)-1 (x)= (g-1 ◦ f-1)(x)
  3. (f ◦ g)(x)= h (x)→ f (x)= (h ◦ g -1)(x)

Contoh Soal dan Pembahasan

Agar kalian dapat memahami lebih jelas mengenai fungsi invers, coba kita kerjakan contoh soal berikut ini.

1. Tentukan rumus fungsi invers dari fungsi f(x) = 2x + 6.

Jawab:

jawaban nomor 1

2. Tentukan rumus fungsi invers dari fungsi gambar di bawah ini:

rumus invers

jawaban nomor 2

3. (SIMAK UI 2013 DASAR)

Diketahui f -1 (4x-5) = 3x-1 dan (f -1 ◦ f)(5)= p2 +2p – 10 maka rata-rata dari nilai p adalah…
  1. -4
  2. -2
  3. -1
  4. 1
  5. 4

Jawab:

f (x) = y ↔ f -1 (y) = x
f (5) = y
f –1 (4x-5) = 3x-1
sehingga 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2

Menentukan nilai p

(f– -1 ◦ f)(5) = p2 + 2p-10
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3

Sehingga, rata-rata nilai p yaitu SIMAK UI 2013 DASAR

Jawabannya adalah C

4.  (UN 2004)

Sebuah pemetaan f:R→R dengan (g ◦ f)(x) = 2x2 + 4 x + 5 dan g(x) = 2x + 3. Maka f(x)=…
  1. x2 + 2x + 1
  2. x2 + 2x + 2
  3. 2x2 + x + 2
  4. 2x2 + 4x + 2
  5. 2x2 + 4x + 1

Jawab:

Menentukan f(x)

(g ◦ f)(x) = 2x2 + 4x + 5
g(f(x)) = 2x2 + 4x + 5
2(f(x)) + 3 = 2x2 + 4x + 5
f(x) = x2 + 2x + 1

Jawabannya: A

5. (SNMPTN 2010 Dasar)

Jika g(x – 2) = 2x – 3 dan (f ◦ g)(x – 2) = 4x2 – 8x + 3, maka f(-3) =…
  1. -3
  2. 0
  3. 3
  4. 12
  5. 15

Jawab:

g(x – 2) = 2x – 3
(f ◦ g)(x – 2) = 4x2 – 8x + 3
f(g(x – 2)) = 4x2 – 8x + 3
f(2x – 3) = 4x2 – 8x + 3

Menentukan f(-3)
Jika -3 = 2x – 3 maka x = 0
Sehingga:
f(-3) = 4(0)2 – 8(0) + 3 = 3

Jawabannya: A

6. (SIMAK UI 2012 DASAR)

Misalkan f : R→ R dan g : R→R, f(x) = x + 2 dan (g ◦ f)(x) = 2x2 + 4x – 6, Misalkan juga x1dan x2 adalah akar-akar dari g(x) = 0 maka x1 + 2x2 =…
  1. 0
  2. 1
  3. 3
  4. 4
  5. 5

Jawab:

Menentukan g(x).

(g ◦ f)(x) = 2x2 + 4x – 6
g(f(x)) = 2x2 + 4x – 6
g(x+2) = 2x2 + 4x -6
g(x) = 2(x – 2)2 + 4(x – 2) – 6 = 2x2 – 8x + 8 + 4x – 8 – 6 = 2x2 – 4x – 6

Menentukan x1 + 2x2

g(x) = 0
2x2 – 4x – 6 = 0
x2 – 2x – 3 = 0
(x-3)(x+1) = 0
x1=3 →x2 = -1, jadi 3
x1 = 2x2 = 3+2 (-1) = 1

atau

x1 = -1 → x2 = 3, jadi
x1 + 2x2 = (-1) + 2(3) = 5

Jawabannya: E

Baca juga: Fungsi Rasional

Demikianlah ulasan singkat terkait Fungsi Invers yang dapat kami sampaikan. Semoga ulasan di atas mengenai Fungsi Rasional dapat kalian jadikan sebagai bahan belajar kalian.

The post Fungsi Invers appeared first on Yuksinau.

ARTIKEL PILIHAN PEMBACA :
Memuat...

Kami cukupkan dulu pembahasan tentang » Fungsi Invers - Visi Kedepan. Semoga saja uraian diatas bisa memberikan manfaat untuk kita semua. Tidak lupa kami sampaikan terima kasih karena sudah berkunjung ke situs Visi Kedepan dan membaca ulasan kami hingga selesai. Kami juga menerima kritik dan saran dari Sobat pembaca semuanya. Silahkan sampaikan di kolom komentar dibawah arikel ini. Sampai ketemu di postingan selanjutnya.

Comments

Post a Comment