» Bangun Ruang Sisi Lengkung - Visi Kedepan

Bangun Ruang Sisi Lengkung - Semangat pagi! Semoga hari Anda menyenangkan dan kami ucapkan selamat datang di situs Visi Kedepan yang saat ini sedang Anda baca. Seperti yang tertulis pada judul, kali ini kita akan membahas tentang Bangun Ruang Sisi Lengkung dan tentunya akan sangat menarik.

Mungkin beberapa waktu yang lalu Anda sedang mencari artikel tentang Bangun Ruang Sisi Lengkung di internet dan dari sekian banyak situs yang menyediakan informasi tersebut, Anda memilih untuk berkunjung ke situs ini, maka Anda sudah membuat keputusan yang tepat, karena kita memang akan mengupasnya. Baiklah langsung disimak saja yuk.

Ulasan Lengkap Bangun Ruang Sisi Lengkung

Yang dimaksud sebagai bangun ruang sisi lengkung merupakan bangun ruang yang mempunyai sisi lengkung. Sisi lengkung ini sendiri adalah sisi yang membentuk lengkungan kurva.

Di dalam materi bangun ruang sisi lengkung hanya terdapat tiga macam bangun ruang yang memiliki sisi lengkung. Diantaranya adalah tabung, kerucut, dan bola.

Dan untuk lebih mudah mengingatnya ketiga bangun sisi lengkung tersebut, kalian dapat memakai jembatan keledai BOTAK, “BOla, TAbung, Kerucut.” Mudah bukan? wkwk.

Sementara dalam materi bangun sendiri, di bagi menjadi dua macam. Yakni bangun ruang sisi datar serta bangun ruang sisi lengkung (yang akan kita bahas di artikel ini).

Dalam bangun ruang sisi datar terdiri atas kubus, balok, prisma, dan limas.

Bangun ruang merupakan suatu bangun tiga dimensi yang memiliki ruang/ volume/ isi dan juga sisi-sisi yang membatasinya.

Macam-macam Bangun Ruang Sisi Lengkung

Seperti yang telah kita jelaskan di atas, bangun ruang sisi lengkung merupakan bangun ruang yang mempunyai sisi lengkung. Sisi lengkung ini sendiri adalah sisi yang membentuk lengkungan kurva.

Dan di dalam bangun ruang sisi lengkung terdapat tiga macam bangun ruang, antara lain:  tabung, kerucut, dan bola.

Berikut adalah penjelasan lebih rinci untuk masing-masing bangun ruang sisi lengkung.

Tabung

Pengertian Tabung

Bangun tabung merupakan suatu bangun ruang tiga dimensi yang mempunyai tutup dan alas yang berbentuk lsebuah ingkaran dengan memiliki ukuran yang sama dan diselimuti oleh persegi panjang.

Unsur-unsur Tabung

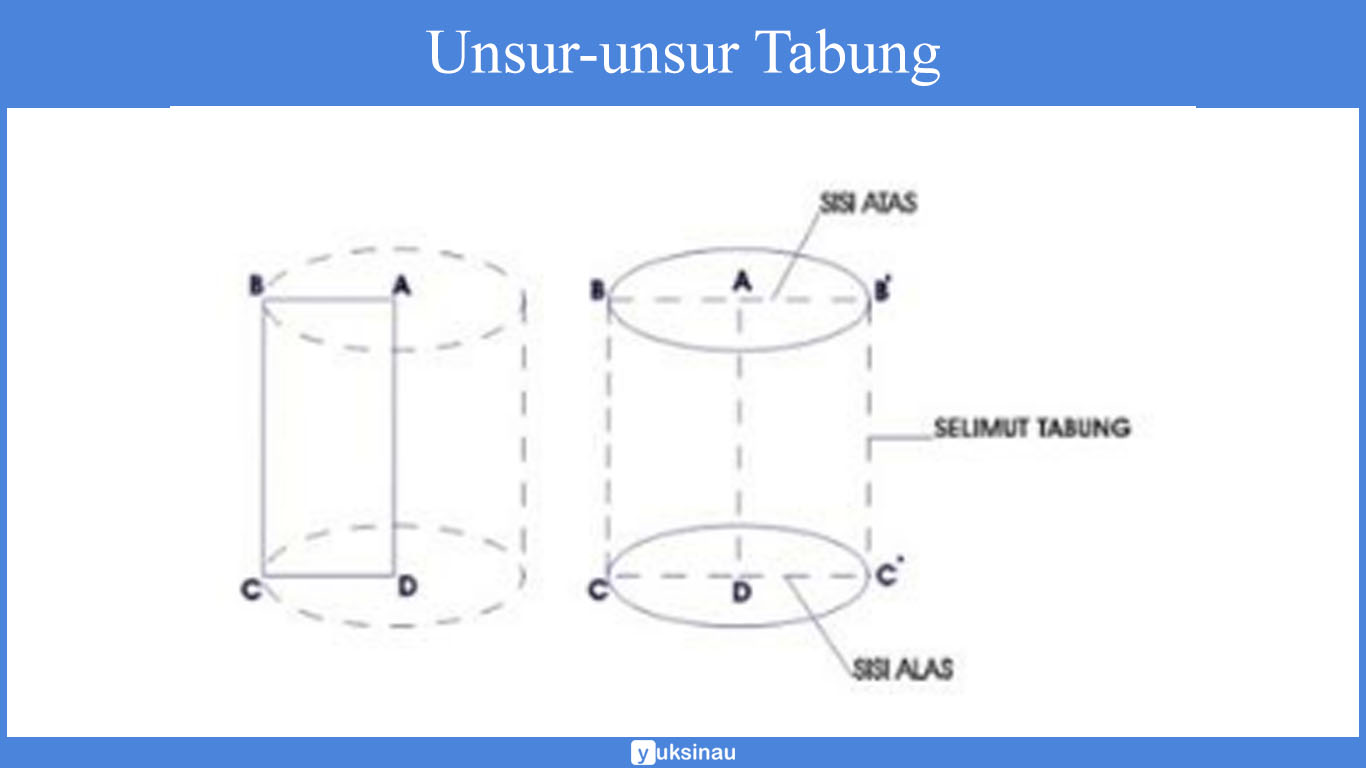
a. Sisi

Tabung memiliki 3 sisi yang berbeda, antara lain yaitu sisi atas, sisi bawah dan sisi lengkung (yang kemudian disebut selimut tabung).

Sisi lengkung tabung merupakan sisi yang dibatasi oleh dua bidang sejajar yakni alas serta atas (tutup) yang berbentuk lingkaran yang kongruen (sama bentuk dan ukurannya). Dan memiliki pusat di A dan D.

b. Tinggi Tabung

Tinggi tabung merupakan jarak antara bidang alas dan juga bidang tutup pada tabung yang biasa dinotasikan dengan menggunakan huruf t. Berdasarkan dari gambar di atas tinggi tabung tersebut yaitu AD.

c. Jari-jari Tabung

Jari-jari lingkaran biasa dinotasikan dengan huruf (r), sisi alas tabung merupakan CD serta sisi tutup tabung merupakan AB.

d. Diameter tabung

Diameter tabung biasa dinotasikan dengan menggunakan huruf (d). Diameter alas tabung yaitu CC’ serta diameter tutup tabung yaitu BB’.

Sifat Tabung

1. Tabung memiliki 3 buah sisi, 1 persegi panjang, 2 lingkaran.
2. Tidak memiliki rusuk.
3. Tidak memiliki titik sudut.
4. Tidak memiliki bidang diagonal.
5. Tidak memiliki diagonal bidang.
6. tabung memiliki sisi alas serta sisi atas berhadapan yang kongruen.
7. Tinggi tabung merupakan jarak titik pusat bidang lingkaran alas dengan titik pusat lingkaran atas.
8. Bidang tegak tabung berwujud lengkungan yang disebut sebagai selimut tabung.
9. Jaring-jaring tabung berwujud 2 buah lingkaran serta 1 persegi panjang.

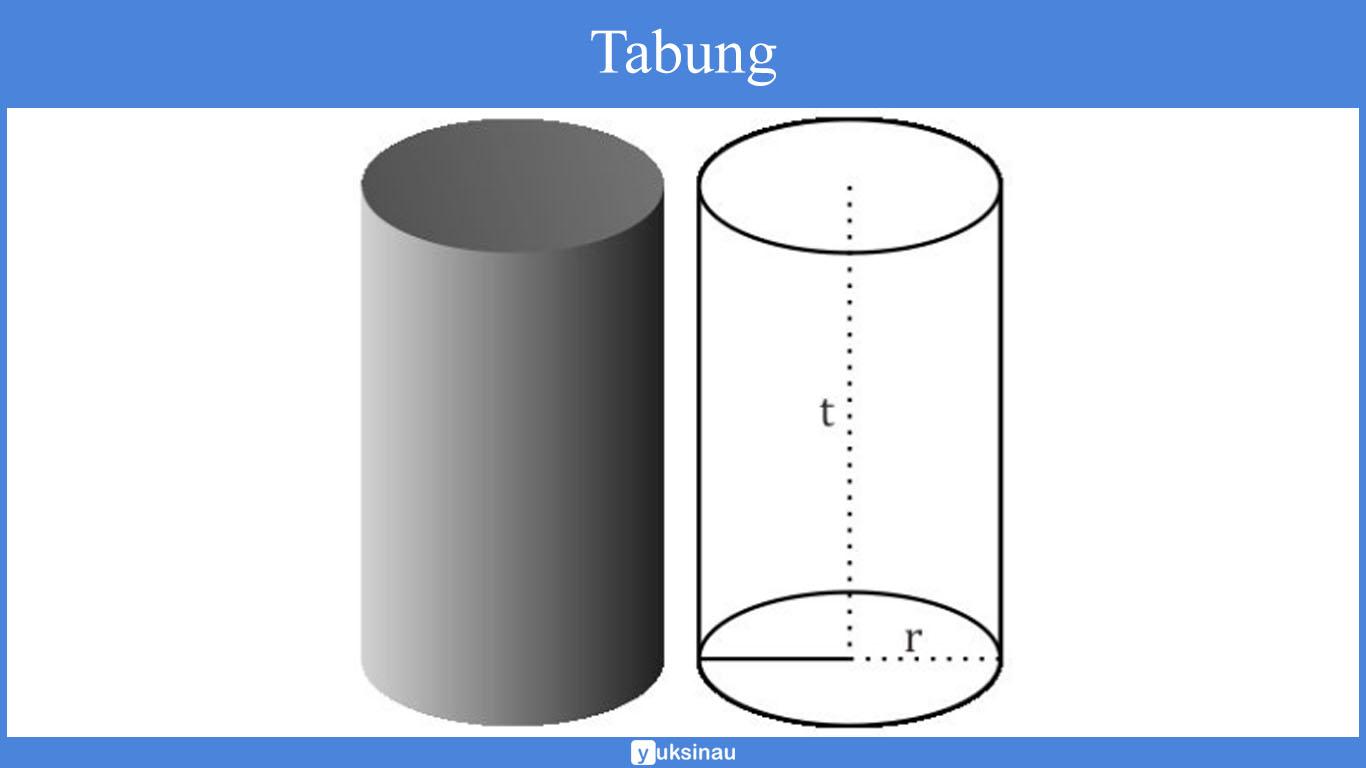
Cara Menggambar Tabung

1. Gambar alas tabung memiliki bentuk ellips atau lonjong yang menunjukkan bahwa alas tersebut merupakan dua buah lingkaran.
2. Lalu tarik garis tegak lurus serta sama panjang di kedua tepi lingkaran.
3. Gambar tutup tabung kongruen dengan sisi alas.
   Jadilah gambar tabung.
   Ingat bahwa terdapat bagian tabung yang tidak nampak dari muka, sebab tidak terlihat maka digambar dengan penggunaan garis putus-putus.
4. Luas Permukaan Tabung
   Tabung apabila kita belah pada sisi tegaknya maka akan nampak sisi lengkungnya yang berupa sebuah persegi panjang serta alas tutupnya ialah bangun lingkaran.

Rumus pada Tabung

• Rumus untuk menghitung luas alas:
  luas lingkaran=π x r²
• Rumus untuk menghitung volume pada tabung:
  π x r² x t
• Rumus untuk menghitung keliling alas pada tabung:
  2 x π x r
• Rumus untuk menghitung luas pada selimut tabung:
  2 x π x r x t
• Rumus untuk menghitung luas pada permukaan tabung:
  2 x luas alas+luas selimut tabung
• Rumus kerucut + tabung:
  • volume = ( π.r².t )+( 1/3.π.r².t )
  • luas = (π.r²)+(2.π.r.t)+(π.r.s)

• Rumus tabung + 1/2 bola:
  • Rumus untuk menghitung Volume = π.r².t+2/3. π.r³
  • Rumus untuk menghitung Luas = (π.r²)+(2.π.r.t)+(½.4.n.r²) = (3.π.r²)+(2. π .r.t)

• Rumus tabung+bola:
  • Rumus untuk menghitung Volume= (π.r².t)+(4/3. π.r³)
  • Rumus untuk menghitung Luas= (2. π.r²)+(4. π.r²) = π.r²

Keterangan:

• V = Volume tabung(cm³)
• π = 22/7 atau 3,14
• r = Jari – jari /setengah diameter (cm)
• t = Tinggi (cm)

Kerucut

Pengertian Kerucut

Kerucut merupakan salah satu bangun ruang yang memiliki sebuah alas yang berbentuk lingkaran dengan selimut yang mempunyai irisan dari lingkaran.

Di dalam geometri, kerucut merupakan sebuah limas istimewa yang memiliki alas lingkaran. Kerucut mempunyai 2 sisi dan 1 rusuk. Sisi tegak kerucut tidak berwujud segitiga namun berwujud bidang miring yang disebut sebagai selimut kerucut.

Yang membedakan antara limas dengan kerucut yaitu alas kerucut memiliki bentuk lingkaran, sementara pada limas berbentuk segi n beraturan.

Kecurut bisa dibentuk dari sebuah segitiag siku-siku yang kalian putar 360^o, dengan sumbu putar pada sisi siku-sikunya.

Unsur-unsur Kerucut

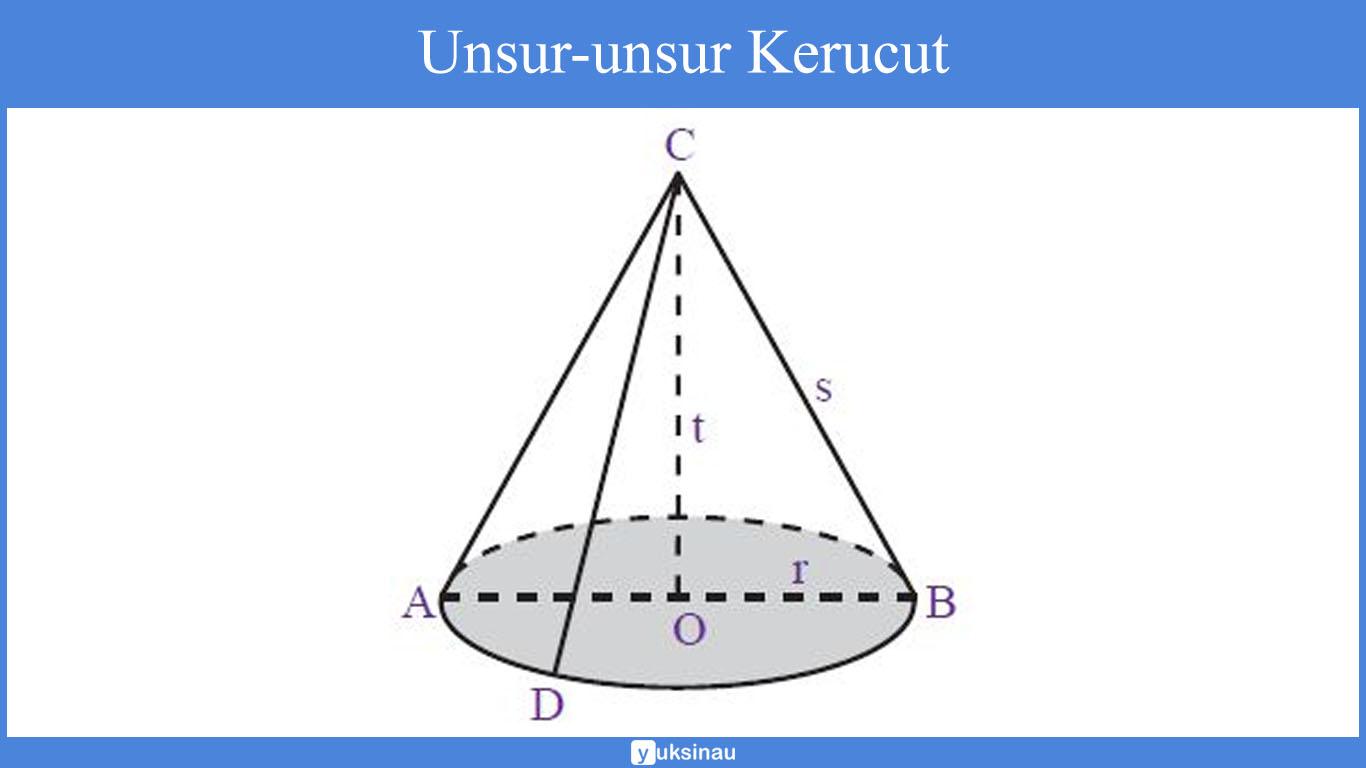
1. Bidang alas, yakni sisi yang berbentuk lingkaran (daerah yang diraster).
2. Diameter bidang alas (d), merupakan ruas garis AB.
3. Jari-jari bidang alas (r), merupakan garis OA serta ruas garis OB.
4. Tinggi kerucut (t), yakni jarak dari titik puncak kerucut ke pusat bidang alas (ruas garis CO).
5. Selimut kerucut, merupakan sisi kerucut yang tidak diraster.
6. Garis pelukis (s), merupakan garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke titik pada lingkaran.

Sifat Kerucut

Terdapat beberapa sifat pada bangun ruang kerucut, antara lain ialah sebagai berikut:

1. Kerucut memiliki 2 sisi.
2. Kerucut tidak  memiliki rusuk.
3. Kerucut memiliki 1 titik sudut.
4. Jaring-jaring kerucut terdiri atas lingkaran serta segitiga.
5. Tidak memiliki bidang diagonal
6. Tidak memiliki diagonal bidang

Rumus pada bangun ruang kerucut

Rumus untuk menghitung volume:
1/3 x π x r x r x t

Rumus untuk menghitung luas:
luas alas+luas selimut

Keterangan:

• r = jari – jari (cm)
• T = tinggi(cm)
• π = 22/7 atau 3,14

Bola

Pengertian Bola

Bola merupakan salah satu bangun ruang sisi lengkung yang dibatasi oleh satu bidang lengkung. Atau juga bisa didefinisikan sebagai sebuah bangun ruang berbentuk setengah lingkaran yang diputar mengelilingi garis tengahnya.

Unsur-unsur Bola

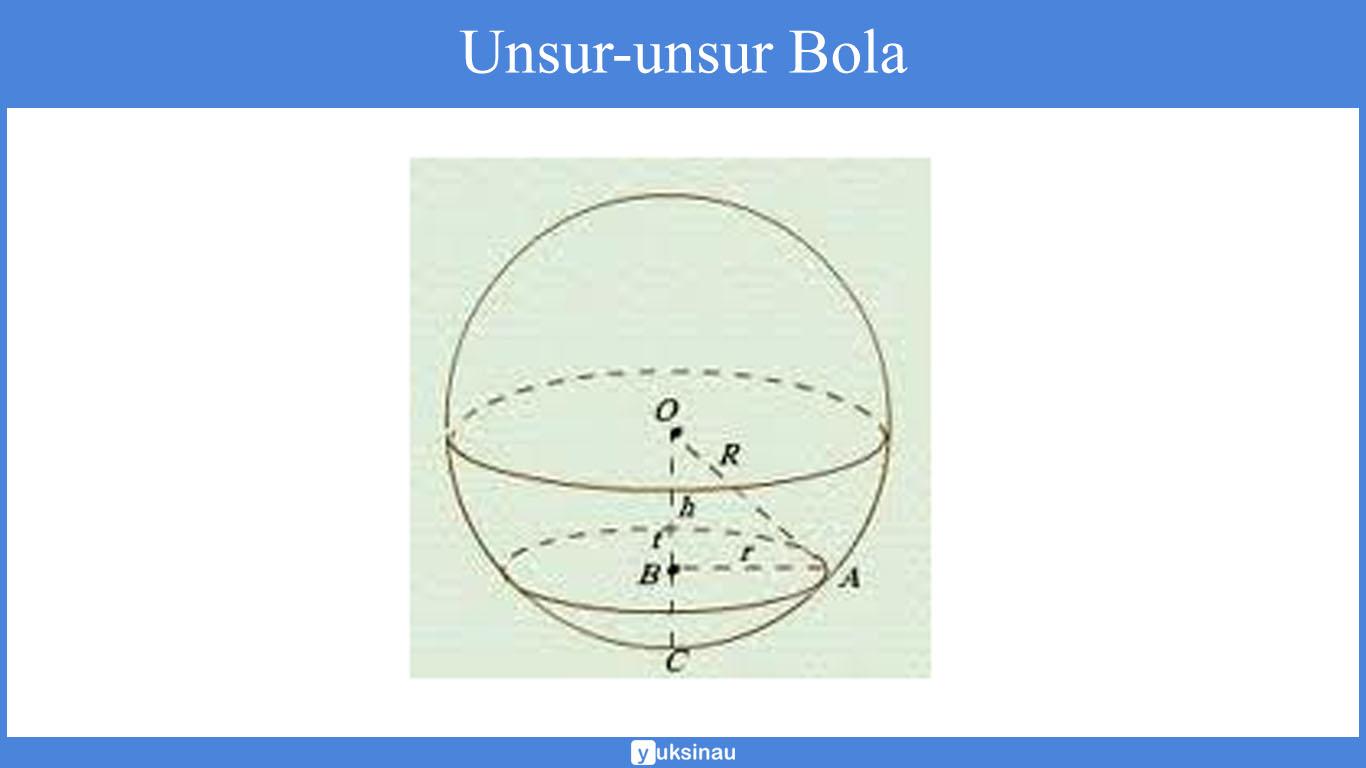
1. Titik O dinamakan titik pusat bola.
2. Ruas garis OA dinamakan sebagai jari-jari bola.
3. Ruas garis CD dinamakan sebagai diameter bola. Apabila kalian perhatikan baik-baik, ruas garis AB juga merupakan diameter bola. AB bisa juga dikatakan sebagai tinggi bola.
4. Sisi bola merupakan sekumpulan titik yang memiliki jarak sama kepada titik O. Sisi tersebut dinamakan sebagai selimut atau kulit bola.
5. Ruas garis ACB dinamakan sebagai tali busur bola.
6. Ruas-ruas garis pada selimut bola yakni ACBDA yang juga dinamakan sebagai garis pelukis bola.

Sifat Bola

1. Bola memiliki 1 sisi serta 1 titik pusat.
2. Bola tidak memiliki rusuk.
3. Bola tidak memiliki titik sudut
4. Tidak memiliki bidang diagonal
5. Tidak memiliki diagonal bidang
6. Sisi bola disebut sebagai dinding bola.
7. Jarak dinding ke titik pusat bola disebut sebagai jari-jari.
8. Jarak dinding ke dinding serta melewati titik pusat disebut sebagai diameter.

Rumus pada Bola

Rumus untuk menghitung volume bola yakni:
4/3 x π x r³

Rumus untuk menghitung luas bola yakni:
4 x π x r²

Keterangan:

V : Volume bola (cm³)
L : Luas permukaan bola (cm²)
R : Jari – jari bola (cm)
π : 22/7 atau 3,14

Baca juga: Kongruen dan Kesebangunan

Contoh Soal dan Pembahasan

Untuk menambah pemahaman pada uraian di atas, maka akan kami berika beberapa contoh soal sekaligus pembahasannya. Simak baik-baik ya.

Soal 1. Kerucut

Tentukan volume kerucut terpancung jika diameter alasnya 10 dm, diameter sisi atas 4 dm, dan tinggi 4 dm! Jari-jari alas = 5dm , Jari-jari atas = 2dm

Gunakan rumus: V = phi×t (R.alas2 + R.alas × R.atas + R.atas2 )

Jawab:

= 3,14×4dm (5dm×5dm + 5dm×2dm + 2dm×2dm)
= 12,56dm (25dm2 + 10dm2 + 4dm2)
= 12,56dm (39dm2)
= 12,56dm × 39dm2
= 489,84dm3

Soal 2. Kerucut

Sebuah kerucut mempunyai tinggi 8 cm serta jari jarinya 6 cm. Hitunglah luas selimut kerucut, luas permukaan kerucut dan juga volume kerucut!

Jawab:

Diketahui:

• t = 8 cm
• r = 6 cm

Ditanyakan:

• Luas Selimut, Luas Permukaan dan Volume = ?

Penyelesaian:

Langkah pertama adalah mencari nilai s (garis lukis) lewatu rumus dibawah ini:

s² = r² + t²

s² = 6² + 8²

= 36 + 64

= 100

s = √100 = 10 cm

Kemudian, kita cari nilai dari luas selimut, luas permukaan dan juga volume kerucutnya dengan cara seperti di bawah ini:

Luas Selimut
= πrs
= 3,14 x 6 x 10
=188,4 cm²

Luas Permukaan
= πr ( s + r )
= 3,14 x 6 (10 + 6)
= 18,84 x 16
= 301,44 cm²

Volume Kerucut
= 1/3  πr²t
= 1/3 x 3.14 x 6² x 8
= 301,44 cm³

Soal 3. Bola

Sebuah balon udara berwujud bola serta terbuat dari bahan elastis. Hitunglah berapa luas bahan yang dibutuhkan untuk membuat balon udara tersebut apabila diameternya 28 m dengan π=22/7!

Jawab:

Diketahui:

• d = 28 → r = 14

Ditanyakan:

• Luas ?

Penyelesaian:

L = 4πr²
L = 4×22/7×14×14
L =  2.464 m²

Sehingga, luas bahan yang diperlukan yakni 2.464 m²

Soal 4. Bola dan Tabung

Sebuah bola besi di masukan ke dalam tabung plastik terbuka dengan bagian atasnya.

Tabung tersebut lalu diisi dengan air sampai penuh. Apabila diameter serta tinggi tabung sama dengan diameter bola yakni 60 cm, maka hitunglah volume air yang tertampung oleh tabung!

Jawab:

Volume air yang dapat ditampung tabung sama dengan volume tabung dengan dikurangi volume bola di dalamnya.
dengan r_tabung = 30 cm, r_bola = 30 cm dan t_tabung = 60 cm, sehingga:

V tabung = πr² t
V tabung = 3,14 x 30 x 30 x 60
V tabung = 169 560 cm³

V bola = ⁴/₃ π r³
V bola = ⁴/₃ x 3,14 x 30 x 30 x 30
V bola = 113 040 cm³

V air = V tabung − V bola
V air = 169 560 − 113 040 = 56 520 cm³

Soal 5. Bola

Berapakah volume bola apabila jari jarinya 10 cm?

Jawab:

Diketahui:

• r = 10 cm

Ditanyakan:

• V = ?

Penyelesaian:

V = 4/3 πr³
= 4/3 x 3,14 x 10³
= 4.186,67 cm³

Sehingga volume bola tersebut yaitu 4.186,67 cm³.

Soal 6. Tabung

Panjang jari-jari alas dari suatu tabung yaitu = 10,5 cm serta tingginya = 20 cm. Untuk π = 22/7 hitunglah:

a. Luas selimut tabung

b. Luas tabung tanpa tutup

c. Luas tabung seluruhnya

Jawab:

Diketahui:

• r = 10,5 cm
• t = 20 cm
• π = 22/7

Ditanyakan:

a. Luas selimut ?

b. Luas tabung tanpa tutup ?

c. Luas tabung seluruhnya ?

Jawab:

a. Luas selimut tabung menggunakan rumus: 2πrt, sehingga

Luas selimut tabung = 2 × 22/7 × 10,5 × 20

Luas selimut tabung = 1.320 cm²

b. Luas selimut tanpa tutup menggunakan rumus: πr² + 2πrt, sehingga

Luas selimut tanpa tutup = (22/7×10,5×10,5)+(2×π×10,5×20)

Luas selimut tanpa tutup = 346,5 + 1.320

Luas selimut tanpa tutup = 1.666,5 cm²

c. Luas tabung seluruhnya menggunakan rumus: 2πr(r+t), sehingga

Luas tabung seluruhnya = 2×22/7×10,5×(10,5+20)

Luas tabung seluruhnya = 2.013 cm²

Soal 7. Tabung

Diketahui suatu tabung mempunyai ukuran jari-jari 10 cm serta tinggi 30 cm. Maka hitunglah:

• volume tabung
• luas alas tabung
• luas selimut tabung
• luas permukaan tabung

Jawab:

Volume tabung
V = π r² t
V = 3,14 x 10 x 10 x 30 = 9432 cm³

Luas alas tabung
L = π r²
L = 3,14 x 10 x 10 = 314 cm²

Luas selimut tabung
L = 2 π r t
L = 2 x 3,14 x 10 x 30
L = 1884 cm²

Luas permukaan tabung
Luas permukaan tabung = luas selimut + luas alas + luas tutup (luas tutup = luas alas)
L =  1884 + 314 + 314= 2512 cm²

Baca juga: Bangun Ruang Sisi Datar

Demikianlah ulasan singkat kali ini yang dapat kami sampaikan terkait bangun ruang sisi lengkung. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian ya.

The post Bangun Ruang Sisi Lengkung appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Kami cukupkan dulu pembahasan tentang » Bangun Ruang Sisi Lengkung - Visi Kedepan. Semoga saja uraian diatas bisa memberikan manfaat untuk kita semua. Tidak lupa kami sampaikan terima kasih karena sudah berkunjung ke situs Visi Kedepan dan membaca ulasan kami hingga selesai. Kami juga menerima kritik dan saran dari Sobat pembaca semuanya. Silahkan sampaikan di kolom komentar dibawah arikel ini. Sampai ketemu di postingan selanjutnya.