Mungkin beberapa waktu yang lalu Anda sedang mencari artikel tentang Fungsi Komposisi di internet dan dari sekian banyak situs yang menyediakan informasi tersebut, Anda memilih untuk berkunjung ke situs ini, maka Anda sudah membuat keputusan yang tepat, karena kita memang akan mengupasnya. Baiklah langsung disimak saja yuk.
Ulasan Lengkap Fungsi Komposisi
Fungsi komposisi merupakan suatu penggabungan dari operasi pada dua jenis fungsi f (x) dan g (x) sampai bisa menghasilkan fungsi baru.
Operasi fungsi komposisi juga biasa dinotasikan dengan penggunaan huruf atau simbol “o” yang dibaca sebagai komposisi atau bundaran.
Fungsi baru yang dapat terbentuk dari f (x) dan juga g (x), yakni:
- (f o g)(x) = g dimasukkan ke f
- (g o f)(x) = f dimasukkan ke g
Dalam fugsi komposisi juga dikenal dengan istilah fungsi tungal. Apa itu fungsi tunggal?
Fungsi tunggal sendiri adalah fungsi yang bisa dilambangkan dengan penggunaan huruf “f o g” maupun juga bisa dibaca sebagai“fungsi f bundaran g”.
Fungsi “f o g” ini merupakan suatu fungsi g yang dikerjakan terlebih dahulu kemudian dilanjutkan dengan f.
Sementara, untuk fungsi “g o f” dibaca sebagai fungsi g bundaran f. Sehingga, “g o f” merupakan suatu fungsi dengan f dikerjakan terlebih dahulu daripada g.
Untuk mempermudah pemahaman dari uraian di atas, simak ulasan selengkapnya mengenai fungsi komposisi di bawah ini.
Fungsi Komposisi
Seperti yang tela disebutkan di atas, fungsi komposisi merupakan suatu penggabungan dari suatu operasi dua jenis fungsi f(x) dan juga g(x) sehingga mampu menghasilkan suatu fungsi baru.
Adapun rumus untuk fungsi komposisi, yaitu:
Rumus Fungsi Komposisi
Sperti yang terdapat pada uraian di atas, operasi untuk fungsi komposisi tersebut biasa dinotasikan dengan penggunakan huruf atau simbol “o”.
Di mana simbol tersebut bisa kita baca sebagai komposisi ataupun bundaran. Fungsi baru inilah yang bisa terbentuk dari f(x) dan g(x) yaitu:
1. (f o g)(x) yang berarti g dimasukkan ke f
2. (g o f)(x) yang berarti f dimasukkan ke g
Fungsi tunggal merupakan suatu fungsi yang dapat dinotasikan dengan penggunakan huruf “f o g” atau dapat dibaca “f bundaran g”.
Lalu Fungsi (f o g) (x) = f (g (x)) → fungsi g (x) dikomposisikan sebagai fungsi f (x)
Sementara itu, “g o f” dibaca sebagai fungsi g bundaran f. Sehingga, “g o f” merupakan fungsi f yang diselesaikan terlebih dahulu dari fungsi g.
Agar dapat memahami fungsi ini, perhatikan gambar dibawah ini :
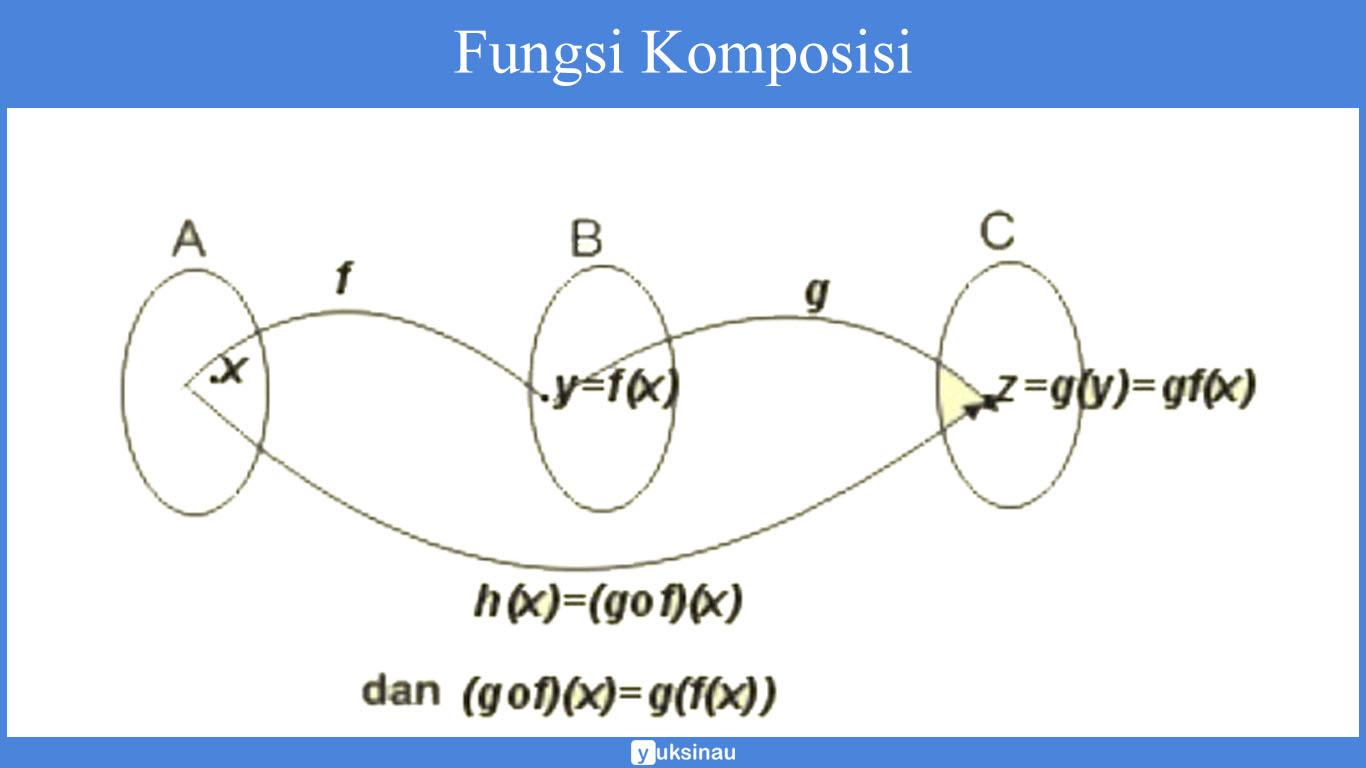
Dari skema rumus di atas, dapat kita ketahui bahawa:
Apabila f : A → B ditentukan dengan menggunakan rumus y = f(x)
Apabila g : B → C ditentukan dengan menggunakan rumus y = g(x)
Sehingga, akan kita peroleh hasil fungsi g dan f yaitu:
h(x) = (gof)(x) = g( f(x))
Dari definisi di atas maka bisa kita simpulkan jika fungsi yang melibatkan fungsi f dan g bisa kita tulis seperti berikut ini:
- (g o f)(x) = g(f(x))
- (f o g)(x) = f(g(x))
Sifat Sifat Fungsi Komposisi
Berikut akan kami berikan beberapa sifat dari fungsi komposisi, diantaranya adalah sebagai berikut:
Apabila f : A → B , g : B → C , h : C → D, maka akan berlaku beberapa sifat seperti:
- (f o g)(x)≠(g o f)(x). Tidak berlaku sifat komutatif.
- [f o (g o h)(x)] = [(f o g ) o h (x)]. Akan bersifat asosiatif.
- Apabila fungsi identitas I(x), maka akan berlaku (f o l)(x) = (l o f)(x) = f(x).
Contoh Soal Fungsi Komposisi
Untuk memahami uraian di atas, berikut akan kami berikan contoh soal untuk fungsi komposisi yang sederhana, perhatikan baik-baik ya.
Soal 1.
Jika diketahui f (x) = 3x + 4 dan g (x) = 3x berapa nilai dari (f o g) (2)?
Jawab:
(f o g) (x) = f (g (x))
= 3 (3x) + 4
= 9x + 4
(f o g) (2) = 9(2) + 4
= 22
Gimana? Mudah bukan?
Fungsi Komposisi pada Kehidupan
Berikut akan kami berikan contoh fungsi komposisi yang ada dalam kehidupan sehari-hari, diantaranya yaitu:
1. Pembuatan buku bisa diproses lewat 2 tahap, antara lain:
- Tahap editorial akan yang nantinya akan dilanjutkan dengan tahap produksi.
- Di dalam tahap editorial, naskah akan kemudian di edit serta di layout menjadi file yang siap untuk dicetak.
- Berikutnya, file diolah dalam tahap produksi mencetaknya supaya menjadi sebuah buku.
- Proses pembuatan buku ini menggunakan penerapan dari algoritma fungsi komposisi.
2. Untuk mendaur ulang logam yakni:
- Pada mulanya pecahan logam campuran akan dijadikan menjadi serpihan kecil.
- Kemudian Drum magnetic yang terdapat di dalam mesin penghancur menyisihkan logam magnetic yang memuat unsure bes.
- Lalu sisa dari pecahan logam dikeruk dan kemudian dipisahkan. Sementara untuk serpihan besi dilebur menjadi baja baru. Proses pendauran ulang logam tersebut menerapkan fungsi komposisi.
Fungsi Invers
Fungsi invers terjadi sebab adanya sebuah fungsi yang dinotasikan dengan f (x) serta memiliki relasi pada setiap himpunan A ke setiap himpunan B.
Sehingga akan menjadi sebuah fungsi invers yang dinotasikan dengan f-1 (x) yang tak lain mempunyai relasi dari himpunan B ke setiap himpunan A.
Sehingga, fungsi invers diperoleah dari f : A → B yang berubah menjadi f-1 B → A sehingga daerah asal atau domain f (x), menjadi daerah kawan atau kodomain menjadi daerah hasil atau range f-1 (x) yakni himpunan A. Begitu pula sebaliknya terjadi pada himpunan B.
Fungsi invers atau yang juga dikenal sebagai fungsi kebalikan adalah sebuah fungsi yang berkebalikan dari fungsi asalnya.
Sebuah fungsi f mempunyai fungsi invers (kebalikan) f-1 jika f adalah fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut bisa dinyatakan seperti berikut:
(f-1)-1 = f
Simplenya, fungsi bijektif berlangsung pada saat jumlah anggota domain sama dengan jumlah anggota kodomain.
Tidak terdapat dua atau lebih domain berbeda dipetakan ke kodomain yang sama. Serta pada setiap kodomain mempunyai pasangan di domain. Perhatikan gambar yang ada di bawah ini:
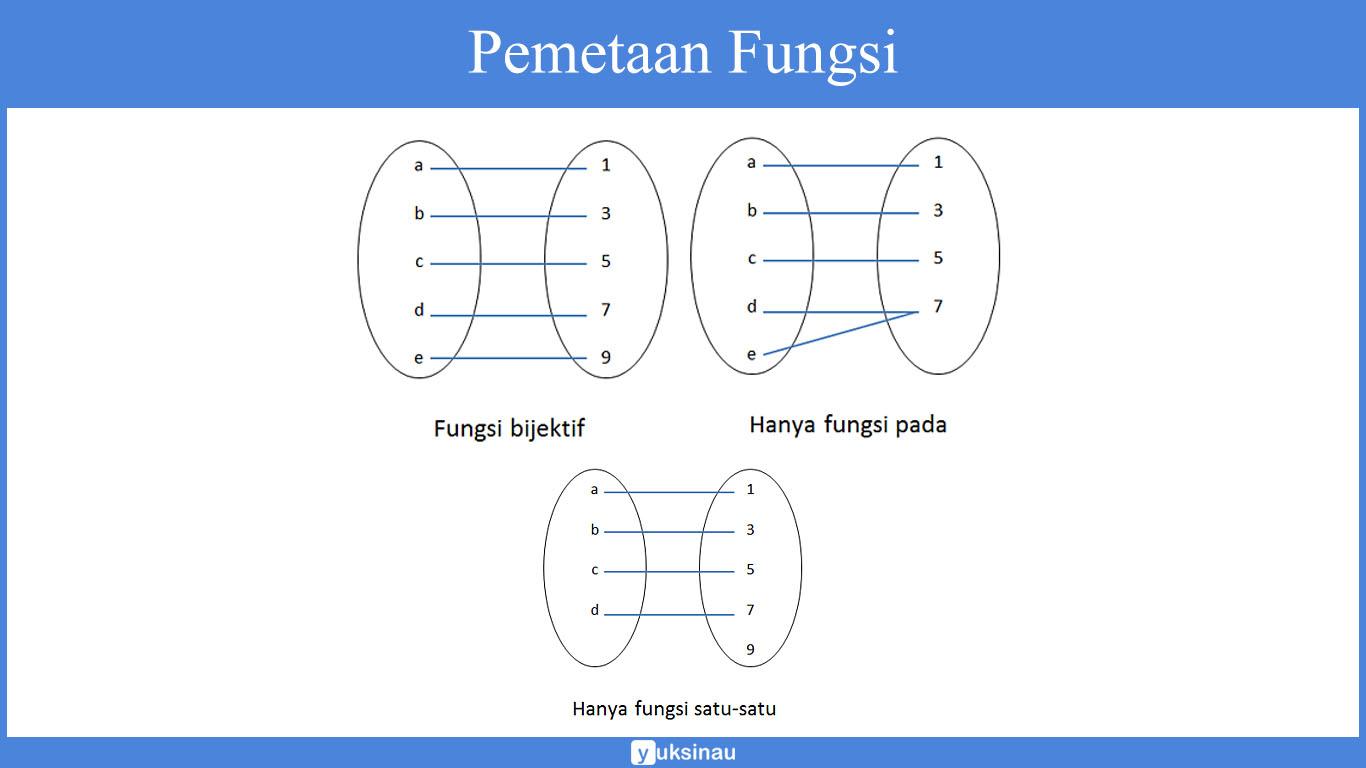
Berdasarkan gambar dari pemetaan di atas, pemetaan pertama menunjukan fungsi bijektif.
Pemetaan kedua bukan merupakan fungsi bijektif sebab pemetaan tersebut hanya berlangsung fungsi pada.
Domain d dan e dipetakan ke anggota kodomain yang sama. Pemetaan ketiga bukan fungsi bijektif sebab pemetaan tersebut hanya berlangsung pada fungsi satu-satu. Kodomain 9 tidak mempunyai pasangan pada anggota domain.
Sebagai contoh, f fungsi yang memetakan x ke y, sehingga bisa kita tulisakan menjadi y = f(x), maka f-1 merupakan fungsi yang memetakan y ke x, ditulis x = f-1(y).
Misalnya f : A →B fungsi bijektif. Invers fungsi f merupakan fungsi yang mengawankan pada masing-masing elemen B dengan tepat satu elemen pada A.
Invers fungsi f juga dinyatakan dengan f-1 seperti di bawah ini:

Terdapat 3 tahapan untuk menentukan fungsi invers, antara lain:
- Ubahlah bentuk y = f(x) menjadi bentuk x = f(y).
- Tuliskan x sebagai f-1(y) sehingga f-1(y) = f(y).
- Ubahlah variabel y dengan x sehingga akan didapatkan rumus fungsi invers f-1(x).
Dalam fungsi invers ada rumus khusus seperti berikut ini:

Fungsi & Komposisi
Aljabar Fungsi
1. Penjumlahan f dan g
(f + g) (x) = f(x) + g(x).
Contoh Soal:
Diketahui f(x) = x + 2 dan g(x) = x2 – 4. Tentukan (f + g)(x).
Jawab:
(f + g)(x) = f(x) + gx)
(f + g)(x)= x + 2 + x2 – 4
(f + g)(x)= x2 + x – 2
2. Pengurangan f dan g
(f – g)(x) = f(x) – g(x).
Contoh soal
Diketahui f(x) = x2 – 3x dan g(x) = 2x + 1. Tentukan (f – g)(x).
Jawab:
(f – g)(x) = f(x) – g(x)
(f – g)(x)= x2 – 3x – (2x + 1)
(f – g)(x)= x2 – 3x – 2x – 1
(f – g)(x)= x2 – 5x – 1
3. Perkalian f dan g
(f . g)(x) = f(x) . g(x).
Contoh soal
Diketahui f(x) = x – 5 dan g(x) = x2 + x. Tentukan (f × g)(x).
Jawab:
(f × g)(x) = f(x) . g(x)
(f × g)(x)= (x – 5)(x2 + x)
(f × g)(x)= x3 + x2 – 5x2 – 5x
(f × g)(x)= x3 – 4x2 – 5x
4. Pembagian f dan g
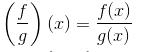
Contoh soal
Diketahui f(x) = x2 – 4 dan g(x) = x + 2. Tentukan
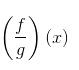
Jawab:
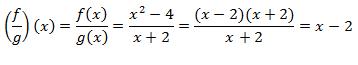
Fungsi Komposisi
Fungsi komposisi bisa kita tuliskan seperti berikut ini:
(f ◦ g)(x) = f (g (x))→ komposisi g (fungsi f bundaran g atau fungsi komposisi dengan g dikerjakan terlebih dahulu daripada f)
gambar 7
(g ◦ f)(x)= g (f (x))→ komposisi f (fungsi g bundaran f atau fungsi komposisi dengan f dikerjakan terlebih dahulu daripada g)
Sifat Fungsi Komposisi
- Tidak berlaku sifat komutatif, (f ◦ g)(x) ≠ (g ◦ f)(x).
- Berlaku sifat asosiatif, (f ◦(g ◦ h))(x) = ((f ◦ g)◦ h)(x).
- Adanya unsur identitas (l)(x), (f ◦ l)(x) = (l ◦ f)(x) = f(x).
Contoh soal:
Diketahui f(x) = 2x – 1, g(x) = x2 + 2. Maka tentukan:
- (g ◦ f)(x).
- (f ◦ g)(x).
- Apakah berlaku sifat komutatif: g ◦ f = f ◦ g?
Jawab:
-
(g ◦ f)(x) = g(f(x)) = g(2x – 1) = (2x – 1)2 + 2 = 4x2 – 4x + 1 + 2 = 4x2 – 4x + 3
-
(f ◦ g)(x) = f(g(x)) = f(x2 + 2) = 2(x2 + 2) – 1 = 4x2 + 4 – 1 = 4x2 + 3
-
Tidak berlaku sifat komutatif sebab g ◦ f ¹ f ◦ g.
Fungsi Invers
1. f-1 (x) adalah invers dari fungsi f(x)
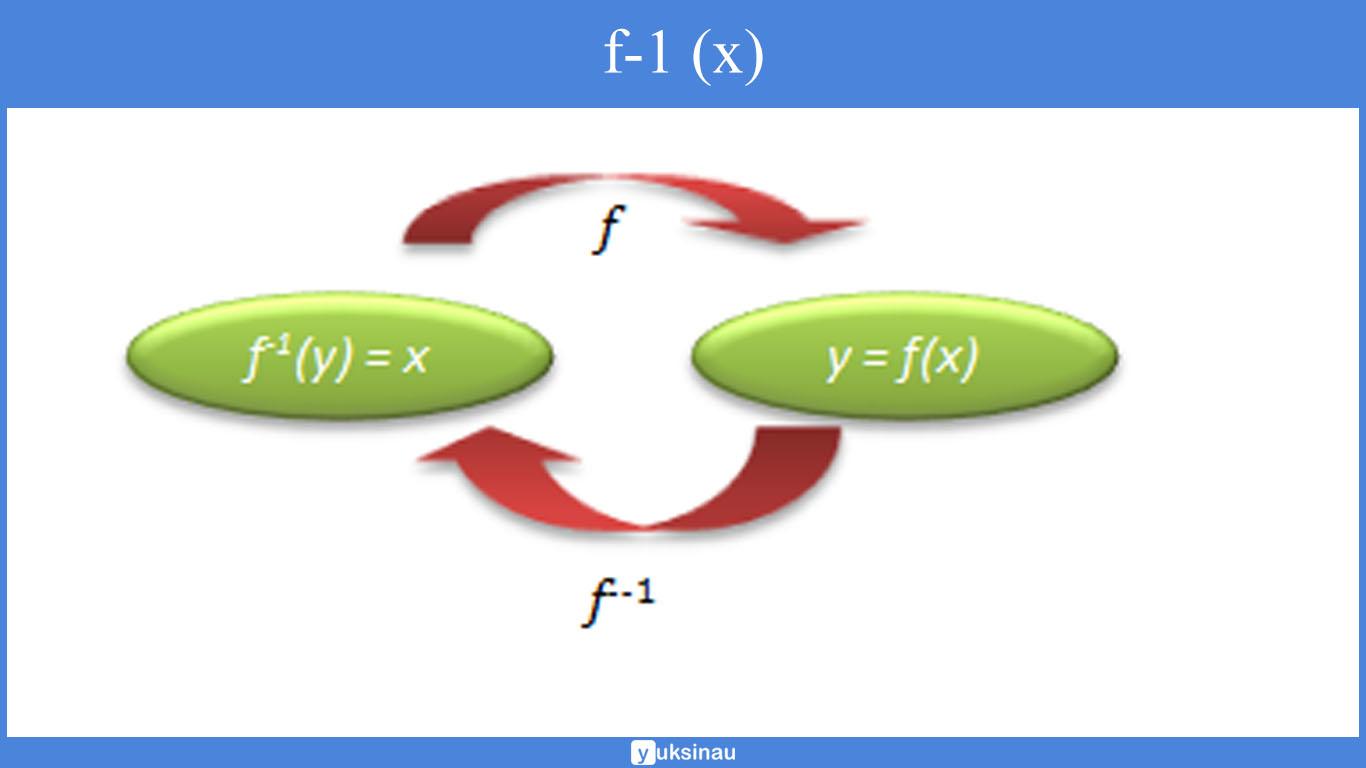
2. Menentukan fungsi invers : mengganti f (x)= y = …” menjadi “ f -1 (y)= x = …”
3. hubungan sifat fungsi invers dengan fungsi komposisi:
- (f ◦ f-1)(x)= (f -1 ◦ f)(x)= l (x)
- (f ◦ g)-1 (x)= (g-1 ◦ f-1)(x)
- (f ◦ g)(x)= h (x)→ f (x)= (h ◦ g -1)(x)
Contoh Soal Fungsi Invers
Untuk memahami uraian di atas, berikut akan kami berikan contoh soal untuk fungsi komposisi yang sederhana, perhatikan baik-baik ya.
Soal 1.
Jika diketahui suatu fungsi f (x) = 5x +20, hitunglah fungsi invers f-1 (x)!
Jawab:
Jika fungsi f (x) dinyatakan dalam bentuk y sama dengan fungsi x → f (x) = y, maka:
f (x) = 5x + 20 → y = 5x + 20
Kemudian, merubah x menjadi f-1 (y), sehingga akan kita dapatkan:
y = 5x + 20
5x = y – 20
x = (y – 20)/5
x = y/5 – 4
f-1 (y) = y/5 – 4
f-1 (x) = x/5 – 4 → sehingga kita dapatkan fungsi invers dari f (x) = 5x + 20
Fungsi Invers dalam Kehidupan
Berikut akan kami berikan contoh fungsi invers yang ada dalam kehidupan sehari-hari, diantaranya yaitu:
1. Dalam Bidang Ilmu fungsi komposisi & inver di terapkan seperti:
- Pada Bidang Ekonomi
Fungsi invers dipakai dalam menghitung sekaligus memperkirakan sesuatu, sebagai contoh fungsi permintaan dan penawaran. - Pada Bidang Kimia
Fungsi ivers digunakan dalam menentukan waktu peluruhan dari suatu unsur. - Pada Bidang Geografi dan Sosiologi
Fungsi invers dipagai dalam optimasi dalam industry dan juga kepadatan penduduk. - Pada Ilmu Fisika
Fungsi invers dipakai untuk persamaan fungsi kuadrat dalam menjelaskan suatu fenomena gerak.
Contoh Soal dan Pembahasan
Setelah kalian memahami dengan baik mengenai fungsi komposisi, yuk coba kita kerjakan contoh soal di bawah ini:
Soal Fungsi Komposisi
Soal 1.
Diberikan dua buah fungsi di mana pada masing-masing f (x) dan g (x) berturut-turut yakni:
f (x) = 3x + 2
g (x) = 2 − x
Maka, tentukan:
a. (f o g) (x)
b. (g o f) (x)
Jawab:
Diketahui:
f (x) = 3x + 2
g (x) = 2 − x
a. (f o g)(x)
“Masukkan g (x) nya ke f (x)”
Sehingga akan kita dapatkan:
(f o g)(x) = f ( g(x) )
= f (2 − x)
= 3 (2 − x) + 2
= 6 − 3x + 2
= − 3x + 8
b. (g o f ) (x)
“Masukkan f (x) nya ke g (x)”
Sehingga akan kita peroleh:
(f o g) (x) = g (f (x) )
= g ( 3x + 2)
= 2 − ( 3x + 2)
= 2 − 3x − 2
= − 3x
Soal 2.
Diketahui suatu fungsi f (x) = 3x − 1 dan juga g (x) = 2×2 + 3. Nilai dari komposisi fungsi ( g o f )(1) yaitu?
A. 12
B. 8
C. 7
D. 11
E. 9
Jawaban
Diketahui:
- f (x) = 3x − 1 dan g (x) = 2×2 + 3
Ditanyakan:
( g o f )(1) =…?
Penyelesaian:
Masukkan f (x) nya ke dalam g (x), kemudian isi dengan 1, sehingga menjadi:
(g o f) (x) = 2 (3 x − 1) 2 + 3
(g o f) (x) = 2 (9 x 2 − 6x + 1) + 3
(g o f) (x) = 18x 2 − 12x + 2 + 3
(g o f) (x) = 18×2 − 12x + 5
(g o f) (1) = 18 (1) 2 − 12(1) + 5 = 11
Jawabannya : D
Soal 3.
Diketehui dua buah fungsi, yaitu sebagai berikut:
f (x) = 2x − 3
g (x) = x2 + 2x + 3
Apabila (f o g)(a) merupakan 33, maka tentukanlah nilai dari 5a!
Jawab:
Langkah pertama adalah mencari terlebih dahulu (f o g)(x), yaitu:
(f o g)(x) sama dengan 2(x2 + 2x + 3) − 3
(f o g)(x) sama dengan 2×2 4x + 6 − 3
(f o g)(x) sama dengan 2×2 4x + 3
33 sama dengan 2a2 4a + 3
2a2 4a − 30 sama dengan 0
a2 + 2a − 15 sama dengan 0
Lalu faktorkan hingga menjadi:
(a + 5)(a − 3) sama dengan 0
a = − 5 maupun a sama dengan 3
sampai kita peroleh:
5a = 5(−5) = −25 atau 5a = 5(3) = 15
Soal 4.
Apabila (f o g)(x) = x² + 3x + 4 serta g(x) = 4x – 5. Tentukan nilai dari f(3)!
Jawab:
(f o g)(x) sama dengan x² + 3x + 4
f (g(x)) sama dengan x² + 3x + 4
g(x) sama dengan 3 Jadi,
4x – 5 sama dengan 3
4x sama dengan 8
x sama dengan 2
f (g(x)) = x² + 3x + 4 serta untuk g(x) sama dengan 3 diperoleh x sama dengan 2
Sehingga kita ketahui: f (3) = 2² + 3 . 2 + 4 = 4 + 6 + 4 = 14
Soal 5. (UN Matematika SMA IPA – 2010 P04)
Diketahui fungsi f(x) = 3x − 1 dan g(x) = 2x2 + 3. Nilai dari komposisi fungsi (g o f)(1) =….
A. 7
B. 9
C. 11
D. 14
E. 17
Jawab:
Diketahui:
- f(x) = 3x − 1 dan g(x) = 2x2 + 3
Ditanyakan:
- (g o f)(1) =…….
Masukkan f(x) nya pada g(x) lalu isi dengan angka 1, sehingga akan menjadi:
(g o f)(x) = 2(3x − 1)2 + 3
(g o f)(x) = 2(9x2 − 6x + 1) + 3
(g o f)(x) = 18x2 − 12x + 2 + 3
(g o f)(x) = 18x2 − 12x + 5
(g o f)(1) = 18(1)2 − 12(1) + 5 = 11
Jawaban: C
Soal 6. (SIMAK UI 2013 DASAR)
a. -4
b. -2
c. -1
d. 1
e. 4
Jawab:
f (x) = y  f -1 (y) = x
f -1 (y) = x
f (5) = y
f –1 (4x-5) = 3x-1
Sehingga akan kita peroleh 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2
Menentukan nilai p
(f– -1 ◦ f)(5) = p2 + 2p-10
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3
Sehingga, rata-rata nilai p adalah (-5) + 3 / 2 = -1
Jawaban: C
Soal Fungsi Invers
Soal 1.
Tentukan rumus fungsi invers dari fungsi f(x) = 2x + 6.
Jawab:

Soal 2.
Tentukan rumus fungsi invers dari fungsi gambar di bawah ini:
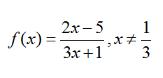

Soal 3. (SIMAK UI 2013 DASAR)
- -4
- -2
- -1
- 1
- 4
Jawab:
f (x) = y  f -1 (y) = x
f -1 (y) = x
f (5) = y
f –1 (4x-5) = 3x-1
sehingga 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2
Menentukan nilai p
(f– -1 ◦ f)(5) = p2 + 2p-10
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3
Sehingga, rata-rata nilai p yaitu 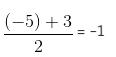
Jawabannya adalah C
Soal 4. (UN 2004)
- x2 + 2x + 1
- x2 + 2x + 2
- 2x2 + x + 2
- 2x2 + 4x + 2
- 2x2 + 4x + 1
Jawab:
Menentukan f(x)
(g ◦ f)(x) = 2x2 + 4x + 5
g(f(x)) = 2x2 + 4x + 5
2(f(x)) + 3 = 2x2 + 4x + 5
f(x) = x2 + 2x + 1
Jawabannya: A
Soal 5. (SNMPTN 2010 Dasar)
- -3
- 0
- 3
- 12
- 15
Jawab:
g(x – 2) = 2x – 3
(f ◦ g)(x – 2) = 4x2 – 8x + 3
f(g(x – 2)) = 4x2 – 8x + 3
f(2x – 3) = 4x2 – 8x + 3
Menentukan f(-3)
Jika -3 = 2x – 3 maka x = 0
Sehingga:
f(-3) = 4(0)2 – 8(0) + 3 = 3
Jawabannya: A
Soal 6. (SIMAK UI 2012 DASAR)
- 0
- 1
- 3
- 4
- 5
Jawab:
Menentukan g(x).
(g ◦ f)(x) = 2x2 + 4x – 6
g(f(x)) = 2x2 + 4x – 6
g(x+2) = 2x2 + 4x -6
g(x) = 2(x – 2)2 + 4(x – 2) – 6 = 2x2 – 8x + 8 + 4x – 8 – 6 = 2x2 – 4x – 6
Menentukan x1 + 2x2
g(x) = 0
2x2 – 4x – 6 = 0
x2 – 2x – 3 = 0
(x-3)(x+1) = 0
x1=3 →x2 = -1, jadi 3
x1 = 2x2 = 3+2 (-1) = 1
atau
x1 = -1 → x2 = 3, jadi
x1 + 2x2 = (-1) + 2(3) = 5
Jawabannya: E
Demikianlah ulasan singkat terkait Fungsi Komposisi yang dapat kami sampaikan. Semoga ulasan di atas mengenai Fungsi Komposisi dapat kalian jadikan sebagai bahan belajar kalian.
The post Fungsi Komposisi appeared first on Tuliskan.
ARTIKEL PILIHAN PEMBACA :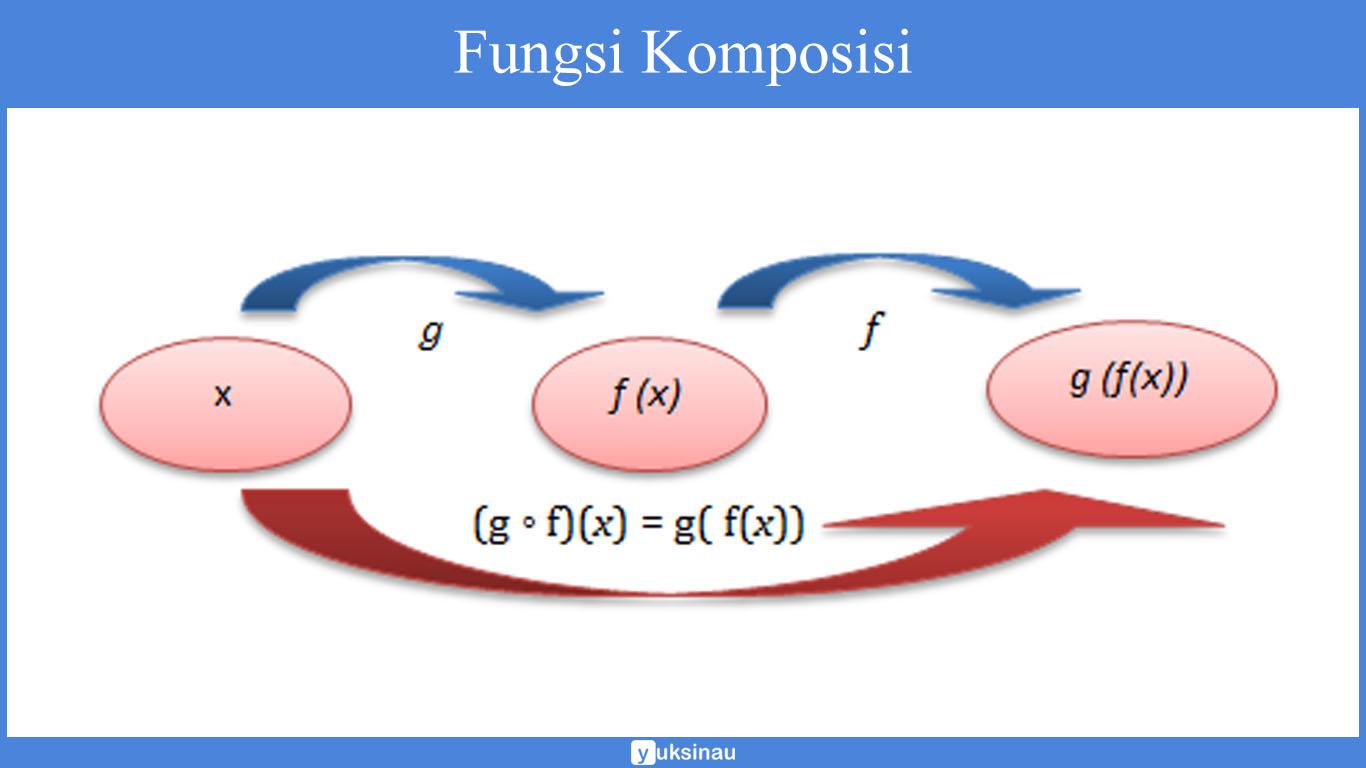
Comments
Post a Comment