» Limit - Visi Kedepan

Limit - Semangat pagi! Semoga hari Anda menyenangkan dan kami ucapkan selamat datang di situs Visi Kedepan yang saat ini sedang Anda baca. Seperti yang tertulis pada judul, kali ini kita akan membahas tentang Limit dan tentunya akan sangat menarik.

Mungkin beberapa waktu yang lalu Anda sedang mencari artikel tentang Limit di internet dan dari sekian banyak situs yang menyediakan informasi tersebut, Anda memilih untuk berkunjung ke situs ini, maka Anda sudah membuat keputusan yang tepat, karena kita memang akan mengupasnya. Baiklah langsung disimak saja yuk.

Ulasan Lengkap Limit

Limit dalam pelajaran matematika merupakan sebuah konsep dalam bidang ilmu matematik yang biasa dipakai untuk menerangkan suatu sifat dari suatu fungsi.

Ketika agumen sudah mendekati pada sebuah titik tak terhingga atau sifat dari suatu barisan saat indeks yang mendekati tak hingga.

Limit pada umumnya digunakan di dalam materi kalkulus serta cabang lainnya dari analisis matematika yang digunakan dalam mencari turunan serta lanjutan.

Dalam pelajaran matematika, limit pada umumnya akan mulai dipelajari ketika pengenalan terhadap kalkulus.

Limit Sebuah fungsi

Jika  f(x) adalah suatu fungsi real serta c merupakan bilangan real, maka bentuk rumusnya adalah:

Maka, sama dengan f(x) bisa kita bikin supaya memiliki nilai sedekat mungkin dengan L dengan cara membuat nilai x dekat dengan c.

Dalam contoh di atas, limit dari f(x) jika x mendekati c, yakni L. Perlu kita ingat, jika kalimat sebelumnya berlaku, walaupun  f(c) ≠ L. Bahkan, fungsi di f(x) tidak perlu terdefinisikan lagi pada titik c.

Berikut merupakan contoh kedua yang menggambarkan sifat.

Sebagai contoh:

Ketika x mendekati nilai 2. Di dalam contoh ini, f(x) memiliki definisi yang jelas di titik ke-2 serta nilainya sama dengan limitnya, yakni 0.4:

f(1.9)	f(1.99)	f(1.999)	f(2)	f(2.001)	f(2.01)	f(2.1)
0.4121	0.4012	0.4001	0.4	0.3998	0.3988	0.3882

Jika x semakin mendekati 2, maka nilai f(x) akan mendekati 0.4, oleh karena itu,

Dalam kasus yang mana f disebut sebagai kontinyu pada x = c. Tetapi, dalam kasus ini tidak selalu berlaku.

Sebagai contoh:

Limit g(x) pada waktu x mendekat 2 yaitu 0.4 (sama seperti f(x), tetapi : g tidak kontinyu pada titik x  =  2.

Atau dapat juga diambil contoh di mana f(x) tidak terdefinisikan pada titik x = c: 

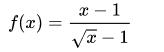
Dalam contoh ini, pada waktu x mendekati 1, f(x) tidak terdefinisikan di titik x = 1 tetapi limitnya sama tetap dengan 2, sebab semakin x mendekati 1, maka f(x) semakin mendekati 2:

f(0.9)	f(0.99)	f(0.999)	f(1.0)	f(1.001)	f(1.01)	f(1.1)
1.95	1.99	1.999	2	2.001	2.010	2.10

Maka dapat kita simbulkan bahawa:

Maka x bisa dibuat sedekat mungkin dengan 1, asal bukan persis sama dengan 1, oleh sebab itu limit darif(x)} f(x) adalah 2.

Definisi Formal Tentang Limit

Definisi formal Limit didefinisikan jika f merupakan fungsi yang terdefinisikan dalam suatu interval terbuka yang mengandung suatu titik  (dengan kemungkinan pengecualian pada titik ) serta L adalah bilangan real. Sehingga;

Itu berarti jika untuk masing-masing diperoleh ∂ > 0 yang untuk seluruh x di mana 0 < | x – c | , maka akan berlaku | f (x) – L | <

Limit Sebuah Fungsi Pada Titik Tak Terhingga

Konsep limit ketika x mendekati tidak terhingga, baik positif maupun negatif merupakan konsep yang berhubungan dengan limit ketika x mendekati suatu angka.

Ini bukan berarti selisih antara x dengan tak terhingga menjadi kecil, sebab tak terhingga bukanlah sebuah bilangan.

Melainkan berarti yakni x menjadi sangat besar untuk tak terhingga atau sangat kecil untuk tak terhingga yang negatif.

Sebagai contoh, perhatikan fungsi di bawah ini:

1. f(100) = 1.9802
2. f(1000) = 1.9980
3. f(10000) = 1.9998

Yakni semakin x bertambah besar, maka nilai f(x)nya akan mendekati 2. Dalam contoh di atas, bisa kita sebut bahwa:

Limit Barisan

Perhatikanlah barisan berikut ini: 1.79, 1.799, 1.7999 …..

Kita bisa melihat jika berbagai angkat di atas mendekati angka 1.8 yakni limit dari barisan tersebut.

Secara formal, contohnya x₁, x₂, … merupakan suatu barisan bilangan riil. Kita katakan bilangan riil (L) sebagai limit barisan ini serta menuliskannya sebagai:

yang itu berarti: Untuk setiap bilangan riil ε > 0 terdapat sebuah bilangan asli n sehingga untuk semuanya: n > n, |x_n − L| < ε.

Secara Intuitif artinya jika pada akhirnya seluruh elemen barisan tersebut akan mendekat sebagaimana yang sudah kita kehendaki kepada limit, sebab nilai absolut |x_n − L| merupakan jarak antara x dan juga L.

Tidak semua barisan mempunya limit. Jika pun ada, kita menyebutnya sebagai konvergen. Dan apabila tidak, disebut sebagai divergen.

Barisan konvergen bisa ditunjukkan bahwa hanya mempunyai satu limit.

Limit barisan serta limit fungsi saling berhubungan erat. Pada satu sisi, limit barisan hanya merupakan limit pada tak terhingga dari sebuah fungsi yang didefinisikan terhadap bilangan asli.

Tetapi di sisi lain, limit suatu fungsi f pada x, jika ada, sama dengan limit barisan x_n = f(x + 1/n).

Limit Fungsi Aljabar

Limit fungsi aljabar adalah salah satu konsep dasar yang ada di dalam kalkulus dan analisis, mengenai kelakuan sebuah fungsi yang mendekati titik masukan tertentu.

Sebuah fungsi memetakan keluaran f(x) untuk masing-masing masukan x. Fungsi tersebut mempunyai limit L pada titik masukan p bila f(x) “dekat” pada L ketika x dekat pada p.

Sehingga dengan sebutan lain, f(x) akan semakin dekat terhadap L pada saat x juga mendekat ke arah p.

Lebih jauh lagi, jika f diterapkan terhadap masing-masing masukan yang cukup dekat pada p, hasilnya merupakan keluaran yang (secara sembarang) dekat dengan L.

Taukah kamu?
Walaupun termasuk secara implisit dalam pengembangan kalkulus di abad ke-17 dan 18, gagasan modern limit fungsi baru dibahas oleh Bolzano di tahun 1817 yang mana memperkenalkan dasar-dasar teknik epsilon-delta. Tetapi karyanya tidak diketahui semasa hidupnya. –sc: wikipedia

Jika masukan yang dekat pada p ternyata dipetakan pada keluaran yang sangat berbeda maka fungsi f akan disebut tidak mempunyai limit.

Definisi limit telah dirumuskan secara formal sejak abad ke-19.

Konsep Limit Fungsi Aljabar

Limit bisa kita definisikan sebagai menuju suatu batas, sesuatu yang dekat tetapi tidak bisa di raih.

Dalam bahasa matematikanya, kondisi tersebut bisa disebut sebagai limit.

Limit adalah suatu konsep matematika di mana sesuatu dikatakan “hampir” atau “mendekati” nilai suatu bilangan tertentu. Limit bisa berwujud suatu fungsi yang kodomainnya “hampir” atau “mendekati” nilai suatu bilangan asli tertentu.

Mengapa harus ada limit? Sebab limit mengungkapkan sebuah fungsi apabila ada batas tertentu didekati.

Mengapa harus didekati? Sebab sebuah fungsi pada umumnya tidak terdefinisi dalam titik-titik tertentu.

Meskipun sebuah fungsi seringkali tidak diartikan pada titik tertentu, tetapi masih bisa dicari tahu berapa nilai yang didekati oleh fungsi tersebut jika titik tertentu semakin didekati yakni dengan limit.

Dalam bahasa matematika, limit ditulis seperti berikut ini:

Artinya, jika x mendekati a tetapi x tidak sama dengan a maka f(x) akan mendekati L. Pendekatan x ke a bisa kita lihat dari dua sisi yakni sisi kiri dan juga sisi kanan atau dengan kata lain x bisa mendekati dari arah kiri dan arah kanan sehingga akan menghasilkan limit kiri dan limit kanan.

Sehingga, dari uraian di atas akan kita peroleh contoh rumus di bawah ini:

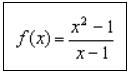
Untuk nilai x yang mendekati 1:

Berikut untuk gambar grafiknya:

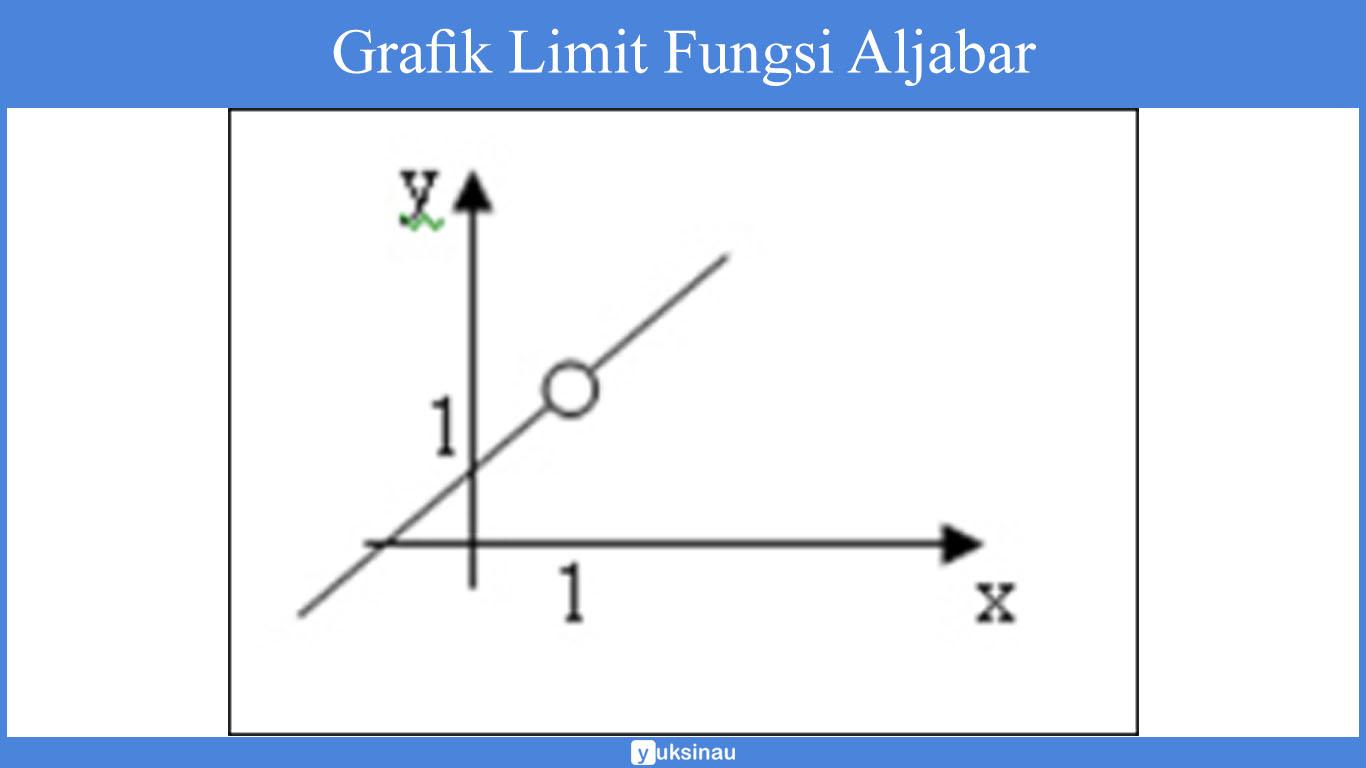
Melihat dari gambar grafik di atas maka dapat diuraikan menjadi:

• Jika x mendekati 1 dari kiri, maka nilai f(x) mendekati 2
  
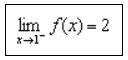
• Jika x mendekati 1 dari kanan, maka nilai f(x) mendekati 2
  
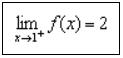
• Sehingga, jika x mendekati 1, maka nilai dari f(x) akan mendekati 2
  

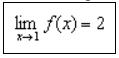
Toerema atau Pernyataan

Sebuah fungsi disebut mempunyai limit jika di antara limit kiri dan limit kananya memiliki besar nilai yang sama. Sehingga, jika limit kiri dan limit kanan tidak sama maka nilai limitnya tidak ada.

Definisi dan Teorema Limit. Seperti yang telah diuraikan di atas, limit dalam bahasa umum berarti batas.

Pada saat kita belajar matematika ada beberapa guru yang menyebutkan jika limit adalah suatu pendekatan.

Artian dari limit ini menyebutkan bahwa sebuah fungsi f(x) akan mendekati nilai tertentu apabila x mendekati nilai tertentu.

Pendekatan ini terbatas antara dua bilangan positif yang sangat kecil yang disebut dengan epsilon dan delta.

Hubungan ke-2 bilangan positif kecil ini akan terangkum dalam definisi limit.

Sifat Sifat Limit Fungsi Aljabar

Jika n adalah suatu bilangan bulat positif, k konstanta, f dan g merupakan suatu fungsi yang memiliki limit di c, maka beberapa sifat di bawah ini akan berlaku.

Macam Macam Metode Penyelesaian Limit Aljabar

Ada beberapa metode atau cara penyelesaian untuk limit aljabar, diantaranya yaitu:

• Metode subitusi
• Metode pemfaktoran
• Metode membagi dengan pangkat tertinggi penyebut
• Metode mengalikan dengan faktor sekawan

Berikut akan kami jelaskan metodenya satu per satu. Simak baik-baik ya.

Menentukan Nilai Limit Fungsi Aljabar

Terdapat 2 jenis untuk menentukan limit fungsi aljabar, diantaranya yakni:

Bentuk yang pertama:

Serta bentuk yang kedua yaitu:

1. Metode Subsitusi

Metode subsitusi hanya akan mengganti peubah yang mendekati nilai tertentu dengan fungsi aljabarnya.

Sebagai contoh:

Sehingga nilai fungsi limit aljabarnya yaitu:

2. Metode Pemfaktoran

Metode pemfaktoran digunakan apabila metode atau cara subsitusi yang menghasilkan nilai limit tidak bisa terdefinisikan.

Sebagai contoh:

Metode pemfaktoran digunakan dengan cara menentukan faktor persekutuan antara pembilang dan penyebutnya.

Dengan hubungannya terhadap bentuk limit kedua terdapat beberapa metode dalam menentukan nilai limit fungsi aljabar yakni metode atau cara membagi dengan pangkat tertinggi penyebut serta metode mengalikan dengan faktor sekawan.

3. Metode Membagi Pangkat Tertinggi Penyebut

Sebagai contoh:

Tentukanlah nilai limit fungsi aljabar dari limit di bawah ini:

 

 

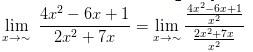
Besar pangkat pembilang serta penyebut dalam soal yakni 2, sehingga,

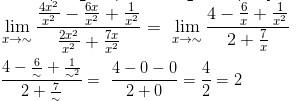
Sehingga, nilai limit fungsi aljabar tersebut yaitu

Contoh soal 2.

Tentukan nilai limit fungsi aljabar dari limit di bawah ini:

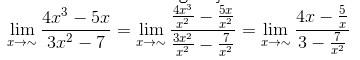
Besar pangkat pembilang dan penyebut dalam soal adalah 3, sehingga,

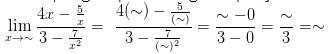
Jadi, nilai dari limit fungsi aljabar tersebut adalah:

4. Metode Mengalikan Dengan Faktor Sekawan

Metode ini dipakai apabila dalam metode substitusi akan langsung menghasilkan nilai limit yang irasional.

Fungsi akan dikalikan dengan akar sekawannya supaya bentuk limit tersebut tidak irasional, sehingga dapat dilakukan kembali substitusi langsung nilai x → c .

Sebagai Contoh:

Limit Fungsi Aljabar Tak Hingga

Dalam pengoprasian limit fungsi aljabar, terkadang juga terdapa nilai x yang mendekati tak berhingga (∞).

Maka dari itu, apabila disubstitusikan fungsinya akan menghasilkan nilai yang tidak menentu.

Dalam pengoperasian limitnya, ada beberapa hukum atau teorema limit yang perlu kalian perhatikan. Apabila n merupakan bilangan bulat, k konstanta, fungsi f dan fungsi g merupakan fungsi-fungsi yang mempunyai nilai limit yang mendekati bilangan c, maka:

Dan terdapat dua metode dalam menyelesaikan limit fungsi aljabar bentuk tak berhingga, antara lain:

1. Membagi dengan pangkat tertinggi

Metode ini dipakai dalam limit fungsi bentuk .

Cara atau metode ini bisa dilakukan dengan cara membagi pembilang f(x) dan penyebut g(x) dengan variabel xⁿ berpangkat tertinggi yang terdapa di dalam fungsi  f(x) dan g(x). Dan kemudian, baru bisa kita substitusikan dengan x → ∞.

Sebagai contoh:

2. Mengalikan bentuk sekawan

Metode ini dipakai pada limit fungsi bentuk . Metode atau cara ini bisa diselesaikan dengan perkalian bentuk sekawan, yaitu:

Lalu dilanjutkan dengan pembagian dengan metode pertama yakni membagi dengan pangkat tertinggi.

Sebagai contoh:

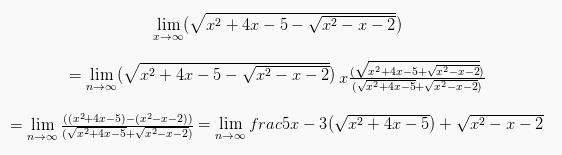
Berikutnya pembilang dan penyebut dibagi pada x pangkat tertinggi yakni x¹:

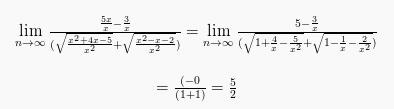
Limit Fungsi Trigonometri

Limit juga bisa dipakai dalam fungsi trigonometri. Penyelesaiannya sama dengan fungsi limit aljabar. Tetapi, supaya paham mengenai penjalasan selanjutnya kalian harus mengerti terlebih dahulu konsep dari trigonometri.

Penyelesaian dalam limit fungsi ini pada trigonometri dapat digunakan dengan cara melakukan beberapa perubahan bentuk sinus, cosinus, dan tangen.

Terdapat tiga bentuk umum dalam limit fungsi trigonometri, diantaranya adalah:

1. Bentuk

Dalam bentuk ini, limit dari fungsi trigonometri f(x) adalah hasil dari substitusi nilai c ke dalam x dari trigonometri.

Sebagai contoh:

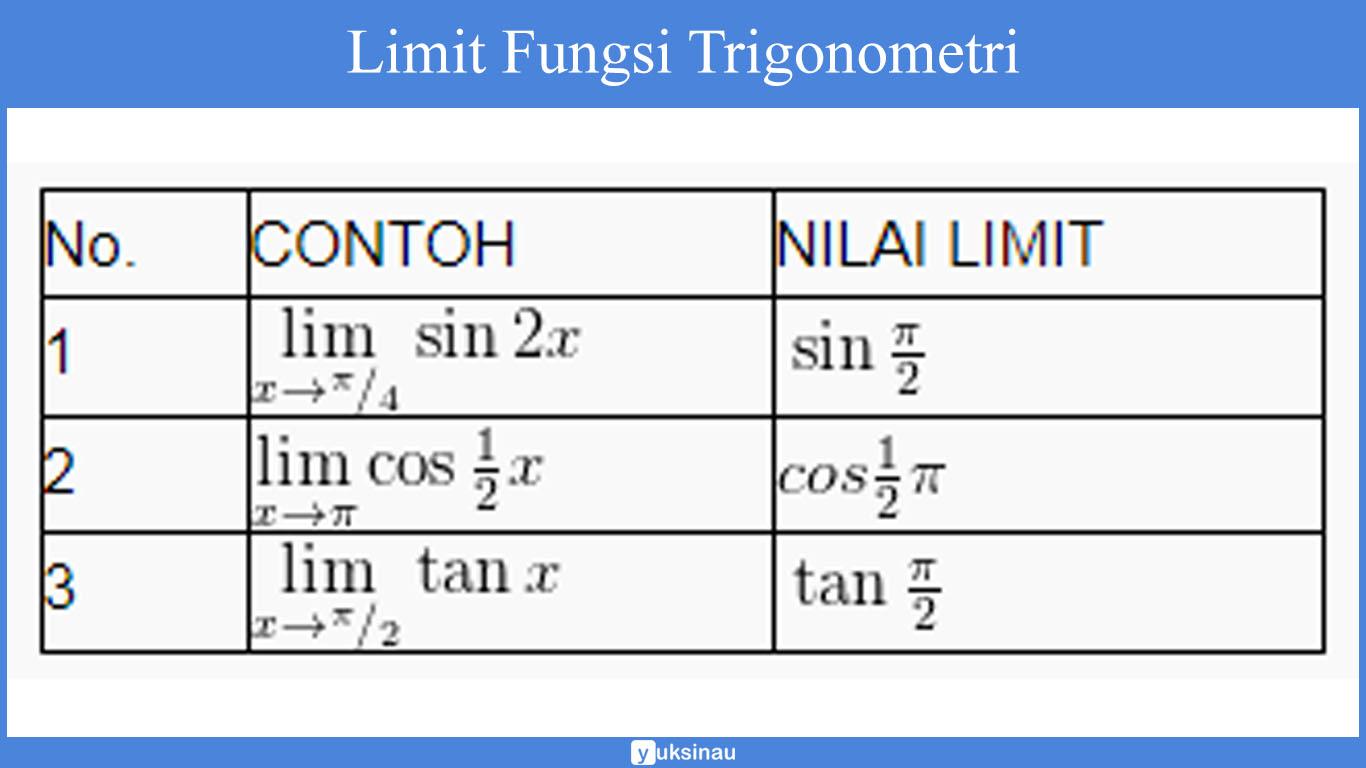
Apabila c = 0, maka rumus limit-limit trigonometrinya yaitu seperti berikut ini:

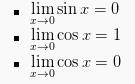
2. Bentuk

Dalam bentuk ini, limit akan didapatkan dari perbandingan 2 trigonometri berbeda.

Kedua trigonometri tersebut apabila langsung disubstitusi dengan nilai c, maka akan menghasilkan f(c) = 0 dan g(c) = 0.

Sehingga, nilai limit trigonometri itu menjadi bilangan tak tentu . Penyelesaiannya sama dengan yang ada pada limit fungsi aljabar yakni pemfaktoran.

Contoh bentuk ini yakni:

3. Bentuk

Dalam bentuk ini, limit didapatkan dari perbandingan antara trigonometri dan fungsi aljabar.

Apabila disubstitusikan langsung akan menghaslikan bilangan tak tentu. Dalam bentuk ini dikerjakan dengan konsep turunan. Bentuk rumus dasar limit ini yaitu:

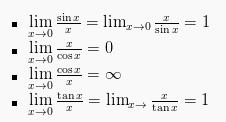
Berdasarkan pada rumus dasar di ataas, apabila dikembangkan lagi akan menjadi rumus-rumus seperti di bawah ini:

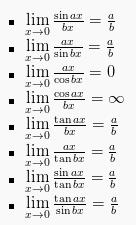
Contoh Soal dan Pembahasan

Cara Mengerjakan Limit Fungsi yang Tidak Terdefinisi

Ada waktnya penggantian nilai x oleh a dalam lim f(x) x→a yang membuat f(x) memiliki nilai yang tidak terdefinisi, atau f(a) menghasilkan bentuk 0/0, ∞/∞ atau 0.∞.

Apabila hal tersebut terjadi, maka solusinya adalah bentuk f(x). Coba kalian sederhanakan supaya nilai limitnya bisa ditentukan.

Limit Bentuk 0/0

Bentuk 0/0 kemungkinan timbul pada:

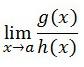
Pada saat kita menjumpai bentuk seperti itu coba untuk utak-utik fungsi tersebut sampai kita mendapati ada bagian yang bisa kita coret.

Apabila itu bentuk persamaan kuadrat kita dapat mencoba memfaktorkan atau dengan cara asosiasi dan jangan lupakan ada aturan a²-b² = (a+b) (a-b).

Berikut akan kami berikan contohnya:

Bentuk ∞/∞

Bentuk limit  ∞/∞ berlangsung pada fungsi suku banyak (polinom) seperti berikut ini:

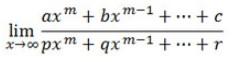
Contoh Soal:

Coba kalian tentukan nilai limit di bawah ini:

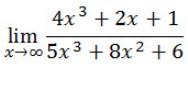
Jawaban:

Berikut adalah rangkuman rumus cepat limit matematika untuk bentuk  ∞/∞

• Apabila m<n maka L = 0
• Apabila m=n maka L = a/p
• Apabila m>n maka L = ∞

Bentuk Limit (∞-∞)

Bentuk (∞-∞) sering sekali muncul pada waktu ujian nasional berlangsung.

Bentuk soalnya sangat ada beberapa macam. Tetapi cara penyelesaiannya tidak jauh dari penyederhanaan. Berikut akan kami berikan contoh soal yang kami ambil dari ujian nasional 2013.

Soal ujian nasional 2013.

Tentukan Limit

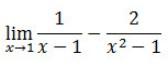
Apabila kalian masukkan x -> 1, maka bentuknya akan menjadi (∞-∞). Serta untuk menghilangkan bentuk ∞-∞ maka kita perlu menyederhanaan bentuk tersebut menjadi,

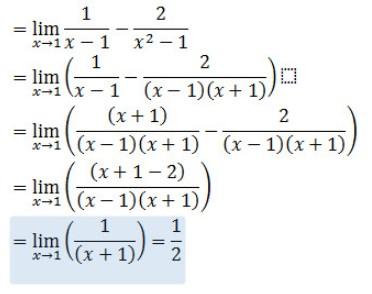
Rumus Cepat menyelesaikan limit tak terhingga

Rumus cepat untuk menyelesaikan limit tak terhingga yang pertama bisa dipakai untuk bentuk soal limit tak terhingga pada bentuk pecahan.

Untuk memperoleh nilai limit tak terhingga dalam bentuk pecahan, kita hanya butuh untuk memperhatikan pangkat tertinggi dari tiap-tiap pembilang dan penyebut.

Terdapat  3 kemungkinan yang bisa saja terjadi.

• Pertama, pangkat tertinggi pembilang lebih kecil dari pangkat tertinggi penyebut.
• Kedua, pangkat tertinggi pembilang sama dengan pangkat tertinggi penyebut.
• Ketiga, pangkat tertinggi pembilang lebih tinggi dari pangkat tertinggi penyebut.

Rumus ke-3 nilai limit tak terhingga bentuk pecahan tersebut bisa kita lihat pada persamaan di bawah ini.

Contoh soal:

Nilai limit dari: 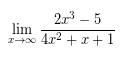adalah …..

A. – ∞

B. – 5

C. 0

D. 5

E. ∞

Pembahasan:

Nilai pangkat tertinggi pada pembilang yaitu 3 dan nilai pangkat tertinggi penyebut yaitu 2 (m>n). Sehingga, nilai limitnya adalah ∞.

Jawabannya: E

Baca juga: Trigonometri

Demikianlah ulasan singkat kali ini yang dapat kami sampaikan mengenai limit matematika. Semoga ulasan di atas mengenai limit matematika dapat kalian jadikan sebagai bahan belajar kalian.

The post Limit appeared first on Tuliskan.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Kami cukupkan dulu pembahasan tentang » Limit - Visi Kedepan. Semoga saja uraian diatas bisa memberikan manfaat untuk kita semua. Tidak lupa kami sampaikan terima kasih karena sudah berkunjung ke situs Visi Kedepan dan membaca ulasan kami hingga selesai. Kami juga menerima kritik dan saran dari Sobat pembaca semuanya. Silahkan sampaikan di kolom komentar dibawah arikel ini. Sampai ketemu di postingan selanjutnya.